
[算法] 八大排序II: 快速、归并、计数、堆排序 的逻辑、复杂度、稳定性详解 - C++实现
快速排序
std::sort(), 在数据量较大但不会超负荷时, 就会采用快速排序逻辑分析
1. Hoare 版
Hoare版的快速排序的思路是什么呢?-
首先, 选择数组的有效范围的头或尾元素, 作为一个
key如果是选择头作为
key, 那么先移动右指针, 直到找到<key的值, 再移动左指针如果是选择尾作为
key, 那么先移动左指针, 直到找到>key的值, 再移动右指针 -
定义
左(left)右(right)指针分别指向数组有效范围的头尾, 并开始向对方靠拢 -
左指针找
>key的数据, 右指针找<key的数据 -
找到之后, 交换两指针指向的数据
-
直到两指针相遇, 然后将所选的
key与相遇位置的数据进行交换 -
key的选择, 一般为数组有效范围的头或尾选择其他位置, 可能需要做特殊处理
key作为分界值, 将数组分为两部分: key左边的数据均<key, key右边的数据均>keykey, 就先移动右指针; 选数组尾作为key, 就先移动左指针key交换位置之后, 依旧满足 key左边的数据均<key, key右边的数据均>key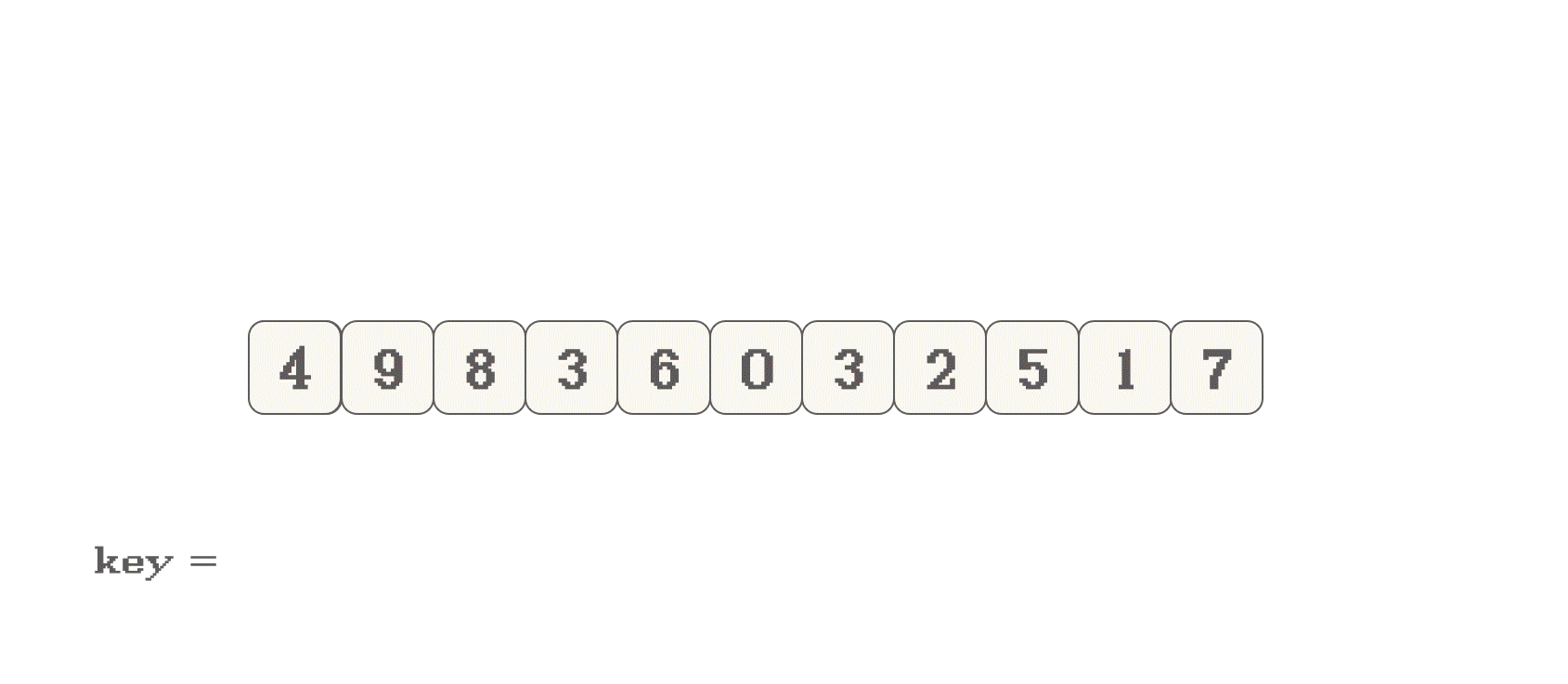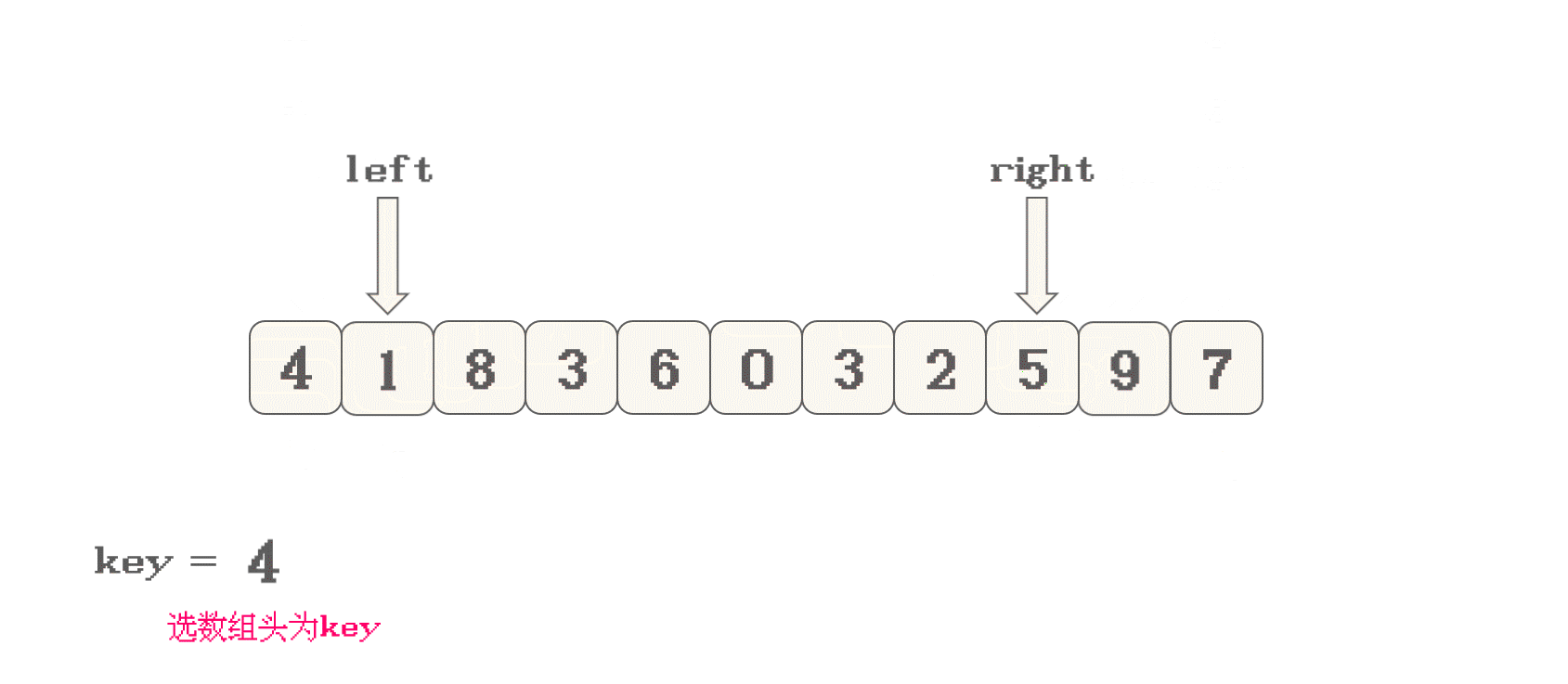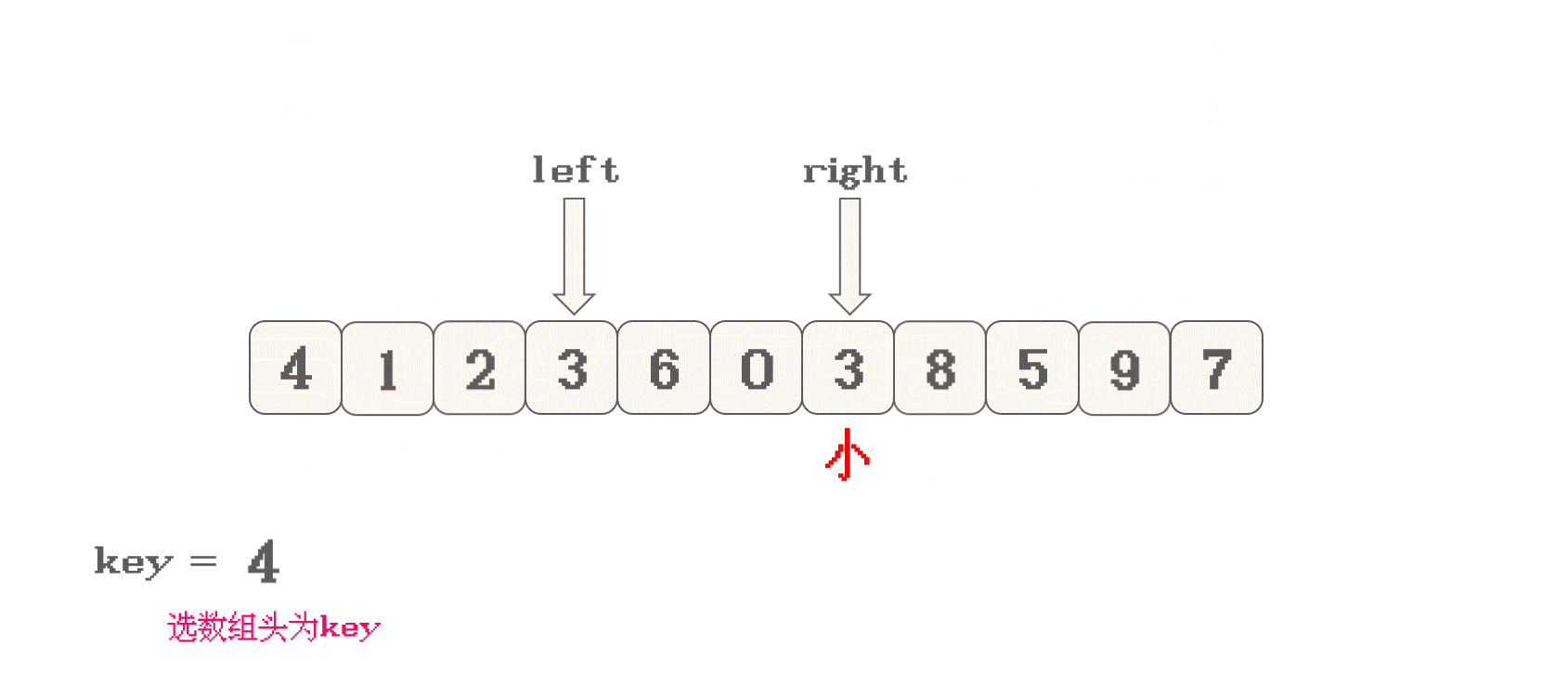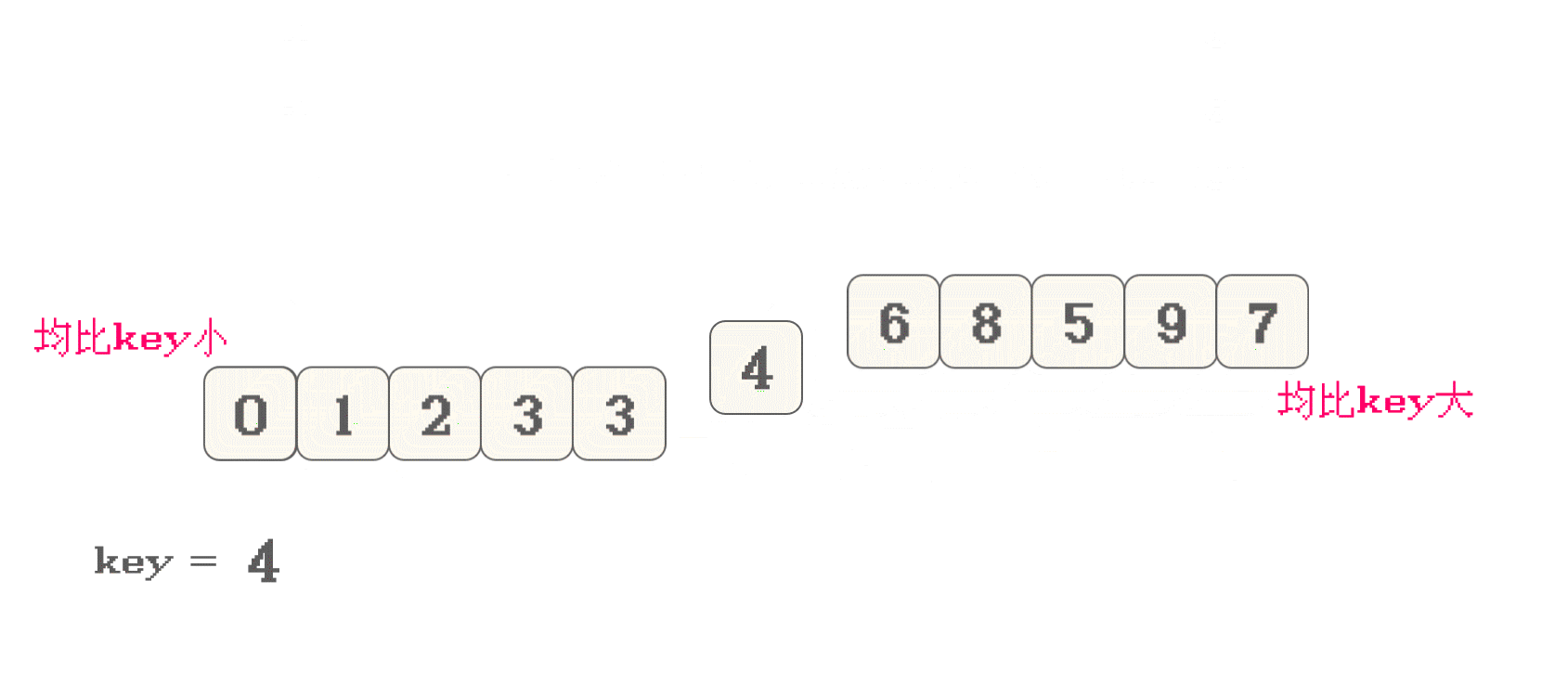
[0, mid-1], 元素均<=nums[mid](key)[mid+1, size], 元素均>=nums[mid](key)- 无论是
left遇到与key相等的值, 还是right遇到与key相等的值, 都可以不停下来, 因为即使停下来交换数据也没有什么意义, 无非就是在mid的左边或右边的区别
Hoare处理之后, 对分出来的左右两部分再次进行相同的处理, 直到最后left和right不再维护一个有效的范围2. 挖坑版
Hoare版不同, 但是目的是相同的-
首先, 将数组有效范围的头或尾看作一个坑
pit, 并将坑值作为key -
定义
左(left)右(right)指针分别指向数组有效范围的头尾如果是选择头作为
key, 那么先移动右指针, 直到找到<key的值如果是选择尾作为
key, 那么先移动左指针, 直到找到>key的值 -
在数组中, 移动
right向左找<key的值 -
right找到目标之后, 将right位置数据放入pit位置, 即 放入坑中, 并 记录right为新的pit -
然后, 开始移动
left向右找>key的值 -
left找到目标之后, 交换left位置数据放入pit位置, 并 记录left为新的pit -
以此为循环, 直到
left与right相遇, 相遇位置为最终的pit -
然后将存储的
key放入最终的pit, 完成一趟排序
left位置是坑, 那么right就找符合条件的数据填坑, 然后right位置就成了新坑right位置是坑, 那么left就找符合条件的数据填坑, 然后left位置就成了新坑key左边数据恒>=key, key右边数据恒<=keyHoare版是相同的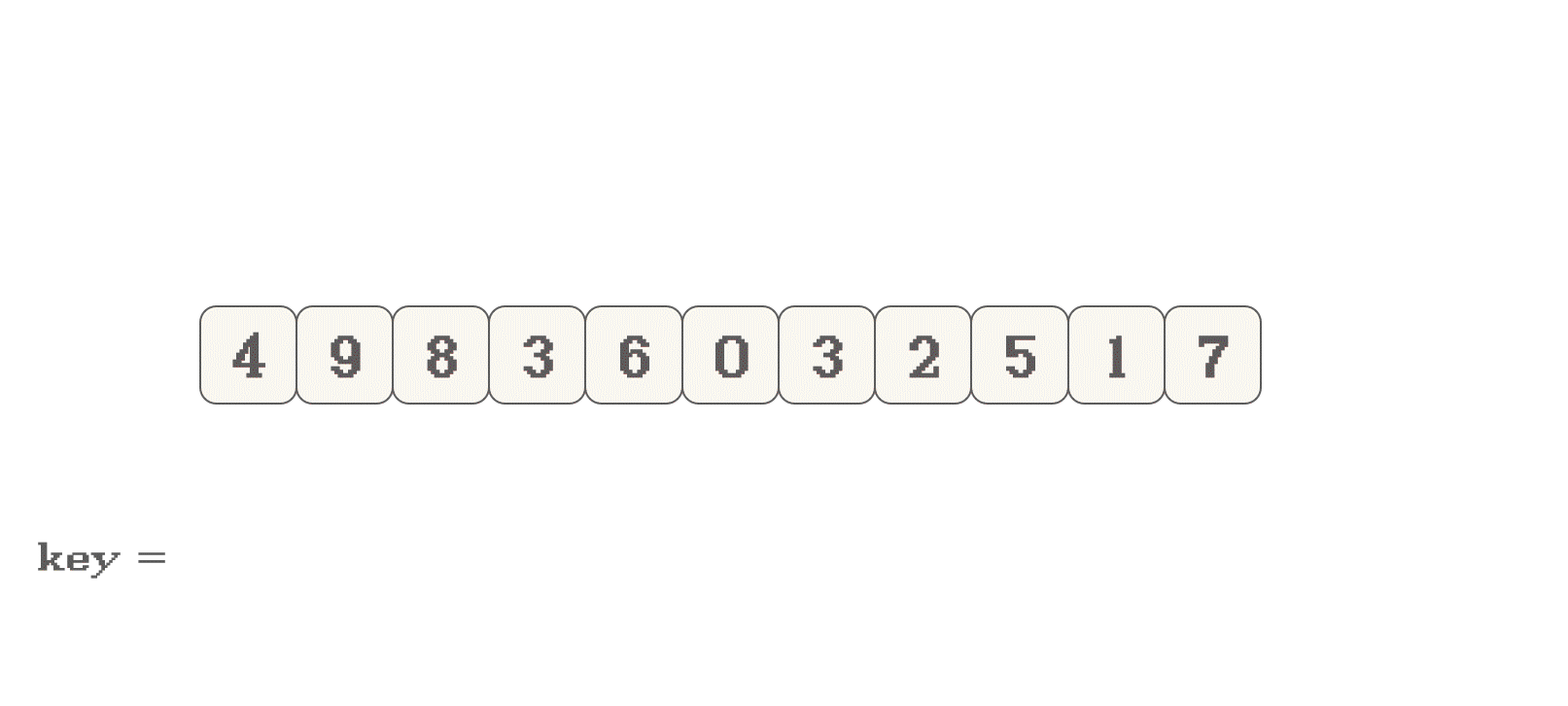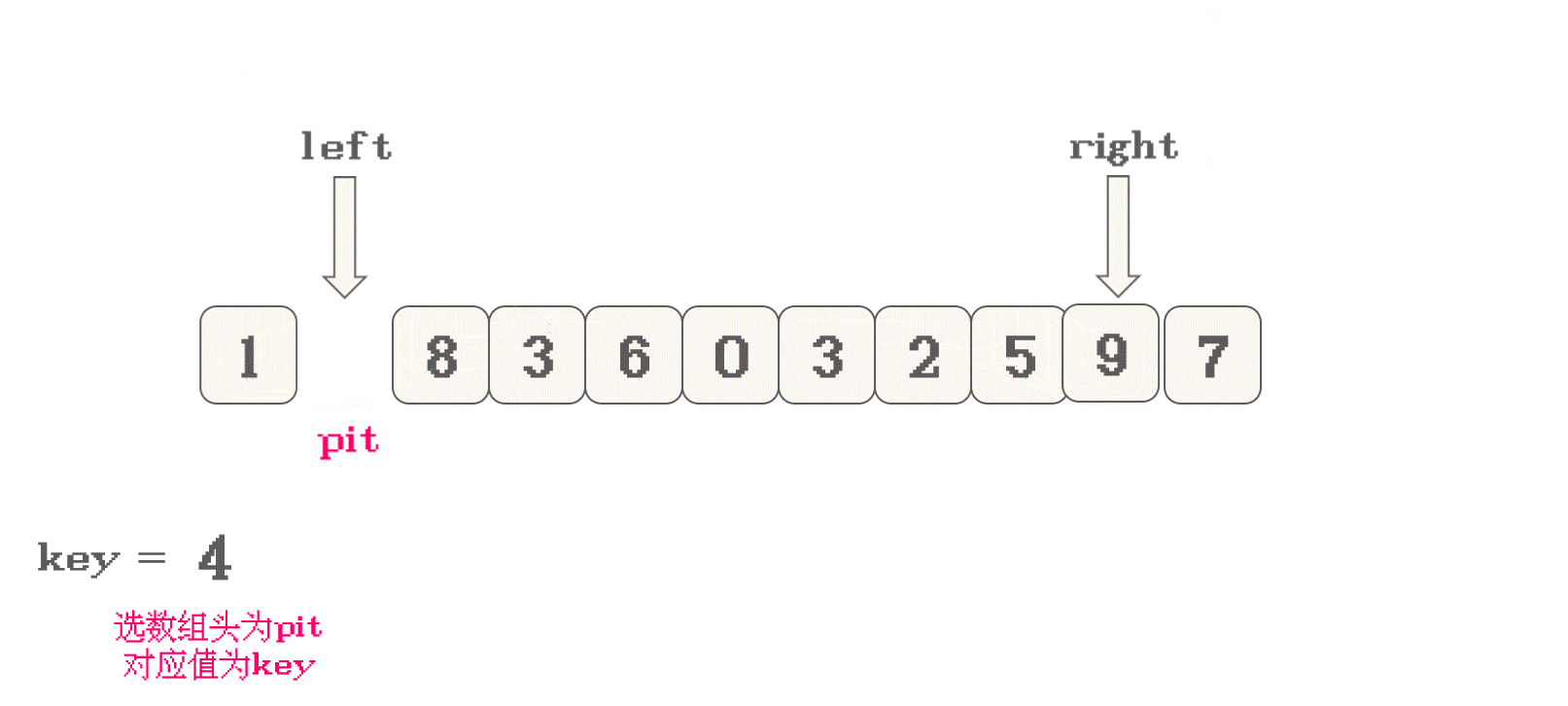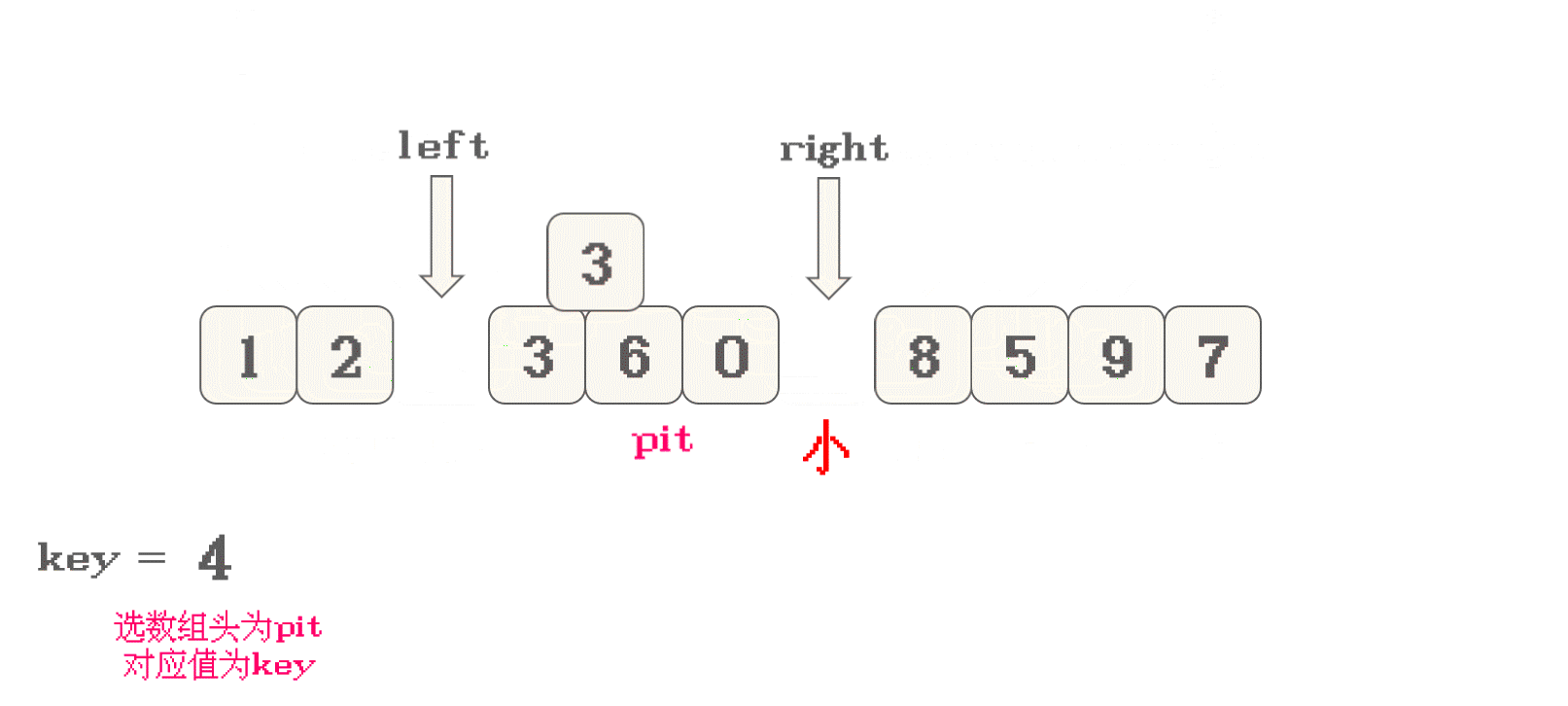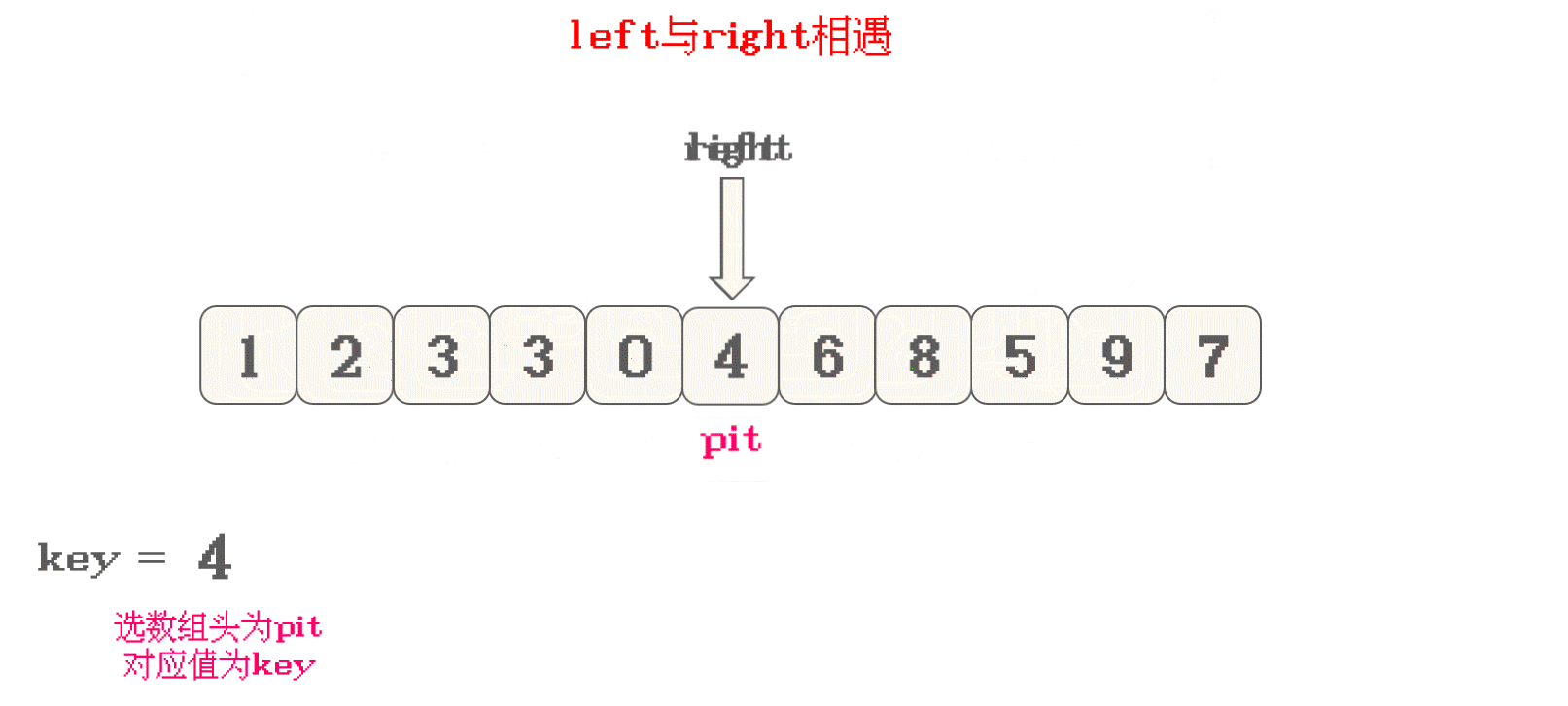
left和right不再维护一个有效范围位置, 整个数组排序完成Hoare版优了一点点, 因为 挖坑版没有执行实质上两个数据的交换, 只有数据覆盖, left和right遇到条件满足的数据之后, 会直接将数据放到pit位置, 不用管pit位置的数据3. 前后指针版
- 首先, 选定数组有效范围的头元素作为
key - 然后, 定义两个指针
last从头位置开始,fast从头+1位置开始 fast向数组尾遍历, 遇到<key的数 停下- 交换
nums[fast]和nums[++last]的数据 - 一直执行此操作, 直到
fast遍历完整个数组 - 然后将 头位置元素与
nums[last]进行交换
<key和>key两部分数据的划分fast从key的下一位开始, 向右找<key的值, last只在交换数据之前++: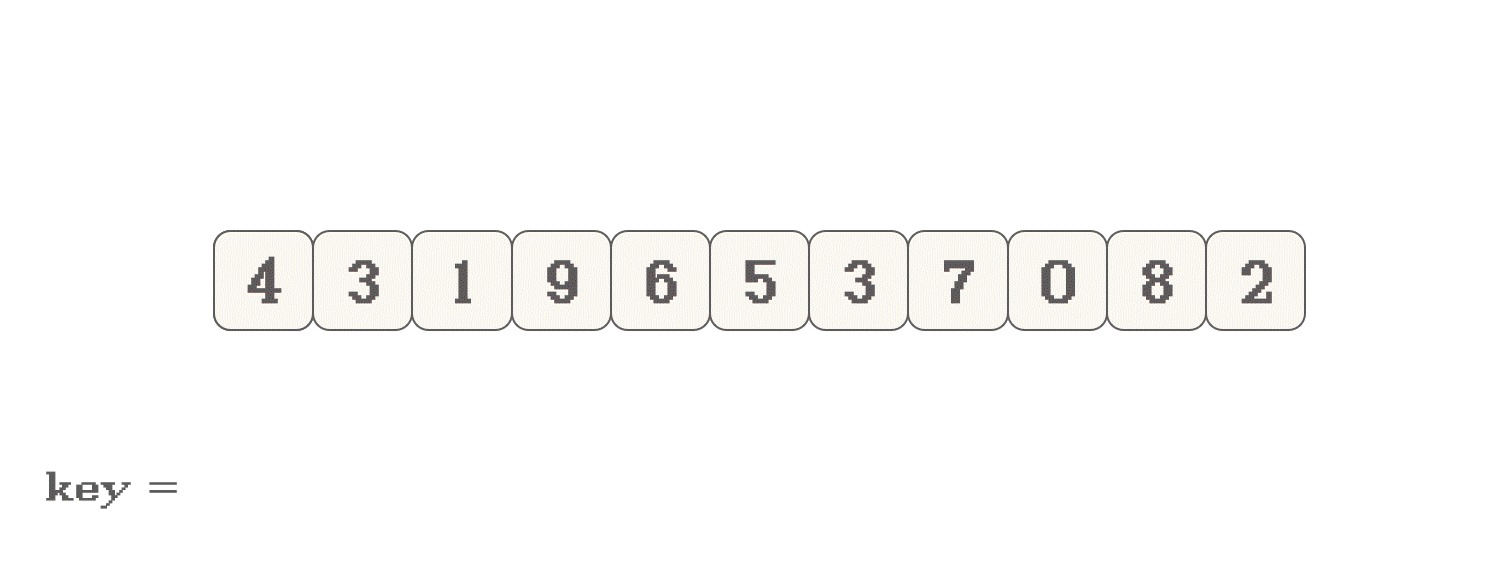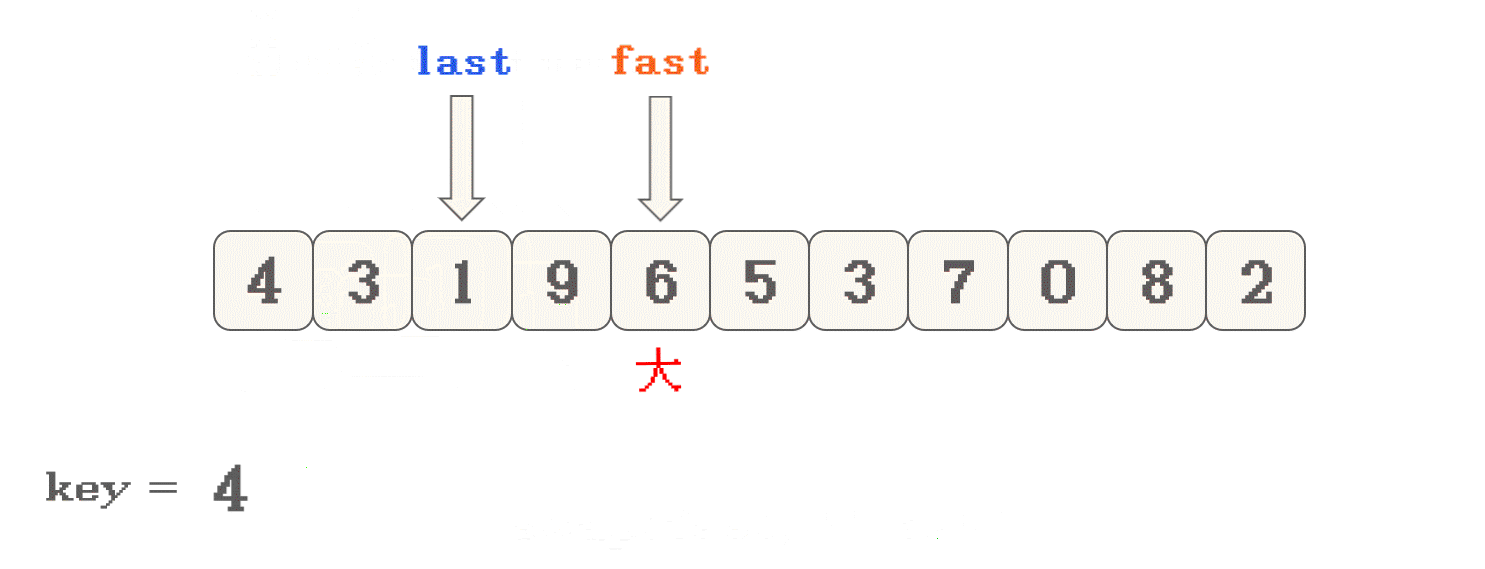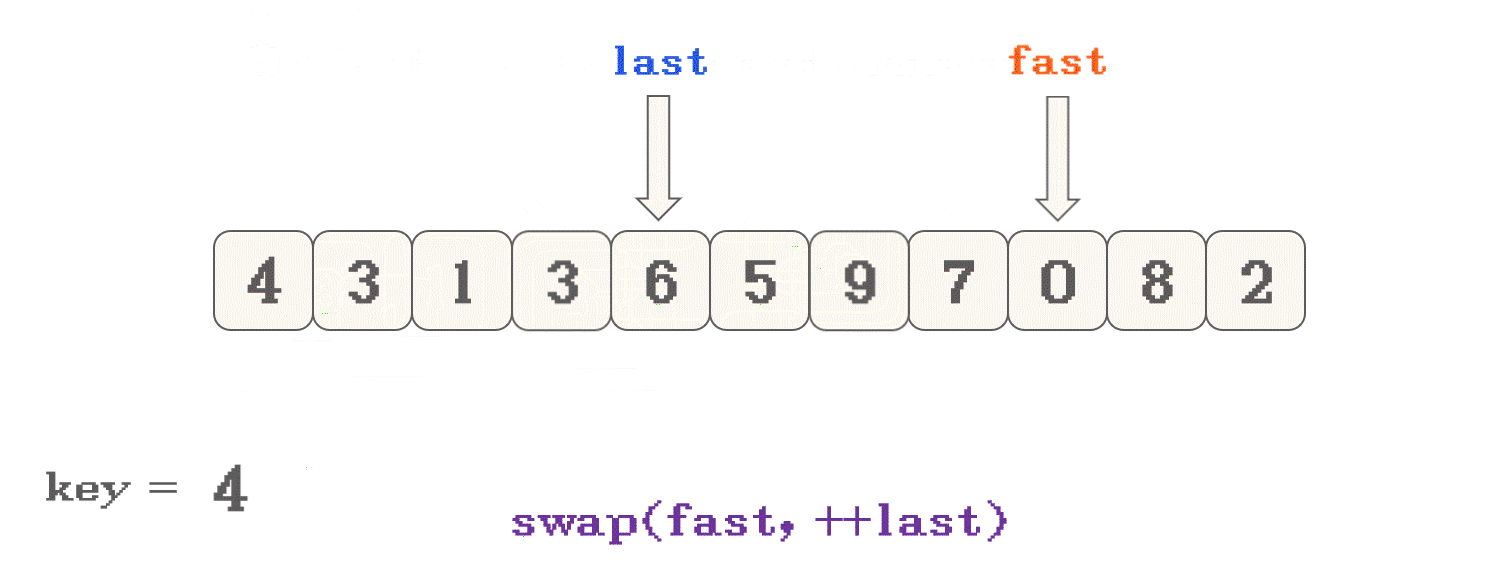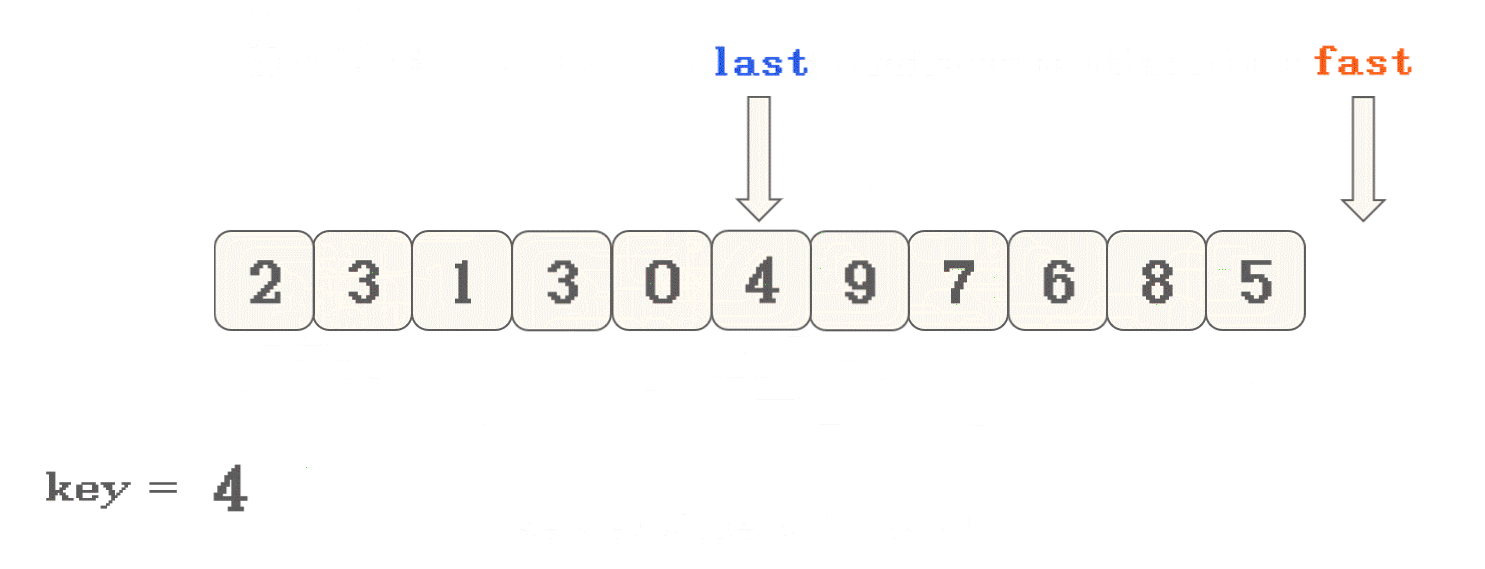
last会有两种位置: 1. 与fast相同的位置; 2. 目前数组中首个>key数据的位置fast还未遇到第一个<key的数据时, 此时 交换数据其实没有意义, 更新移动last才是重点fast遇到第一个<key的数据之后, 此时 才是有效的数据交换代码实现
1. Hoare 版
void numSwap(int& num1, int& num2) {
int tmp = num1;
num1 = num2;
num2 = tmp;
}
// Hoare版
int hoareSortAPart(std::vector<int>& nums, int left, int right) {
int keyi = left;
int key = nums[keyi];
while (left < right) {
while (nums[right] >= key && left < right)
right--;
while (nums[left] <= key && left < right)
left++;
numSwap(nums[left], nums[right]);
}
numSwap(nums[keyi], nums[left]);
return left; // 返回 left, 即两只指针相遇地点, 也就是划分数组界限的位置
}
void _quickSort(std::vector<int>& nums, int begin, int end) {
if (begin >= end) {
return; // 两指针不在维护一个长度>1的有效数组, 返回
}
int keyi = hoareSortAPart(nums, begin, end); // 处理给定范围的数组
_quickSort(nums, begin, keyi - 1); // 处理划分出来 <key的部分
_quickSort(nums, keyi + 1, end); // 处理划分出来 >key的部分
}
void quickSort(std::vector<int>& nums) {
_quickSort(nums, 0, nums.size()-1);
}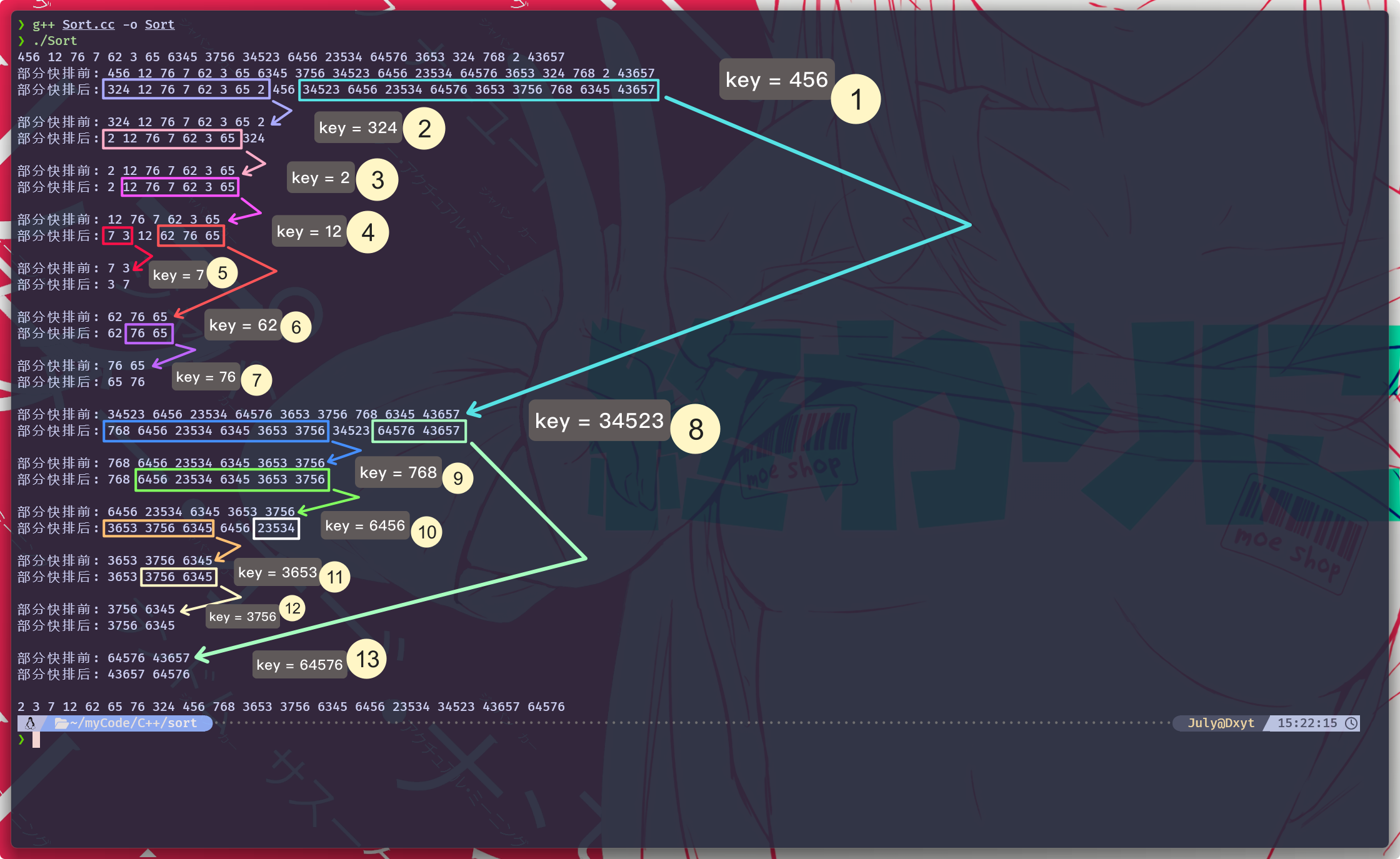
>1时, 不再递归2. 挖坑版
// pit
int pitSortAPart(std::vector<int>& nums, int left, int right) {
int key = nums[left];
int pit = left;
while (left < right) {
while (nums[right] >= key && left < right)
right--;
nums[pit] = nums[right];
pit = right;
while (nums[left] <= key && left < right)
left++;
nums[pit] = nums[left];
pit = left;
}
nums[left] = key; // 相遇位置是最后的坑
return left; // 返回 left, 即两只指针相遇地点, 也就是划分数组界限的位置
}
void _quickSort(std::vector<int>& nums, int begin, int end) {
if (begin >= end) {
return; // 两指针不在维护一个长度>1的有效数组, 返回
}
int keyi = pitSortAPart(nums, begin, end); // 处理给定范围的数组
_quickSort(nums, begin, keyi - 1); // 处理划分出来 <key的部分
_quickSort(nums, keyi + 1, end); // 处理划分出来 >key的部分
}
void quickSort(std::vector<int>& nums) {
_quickSort(nums, 0, nums.size()-1);
}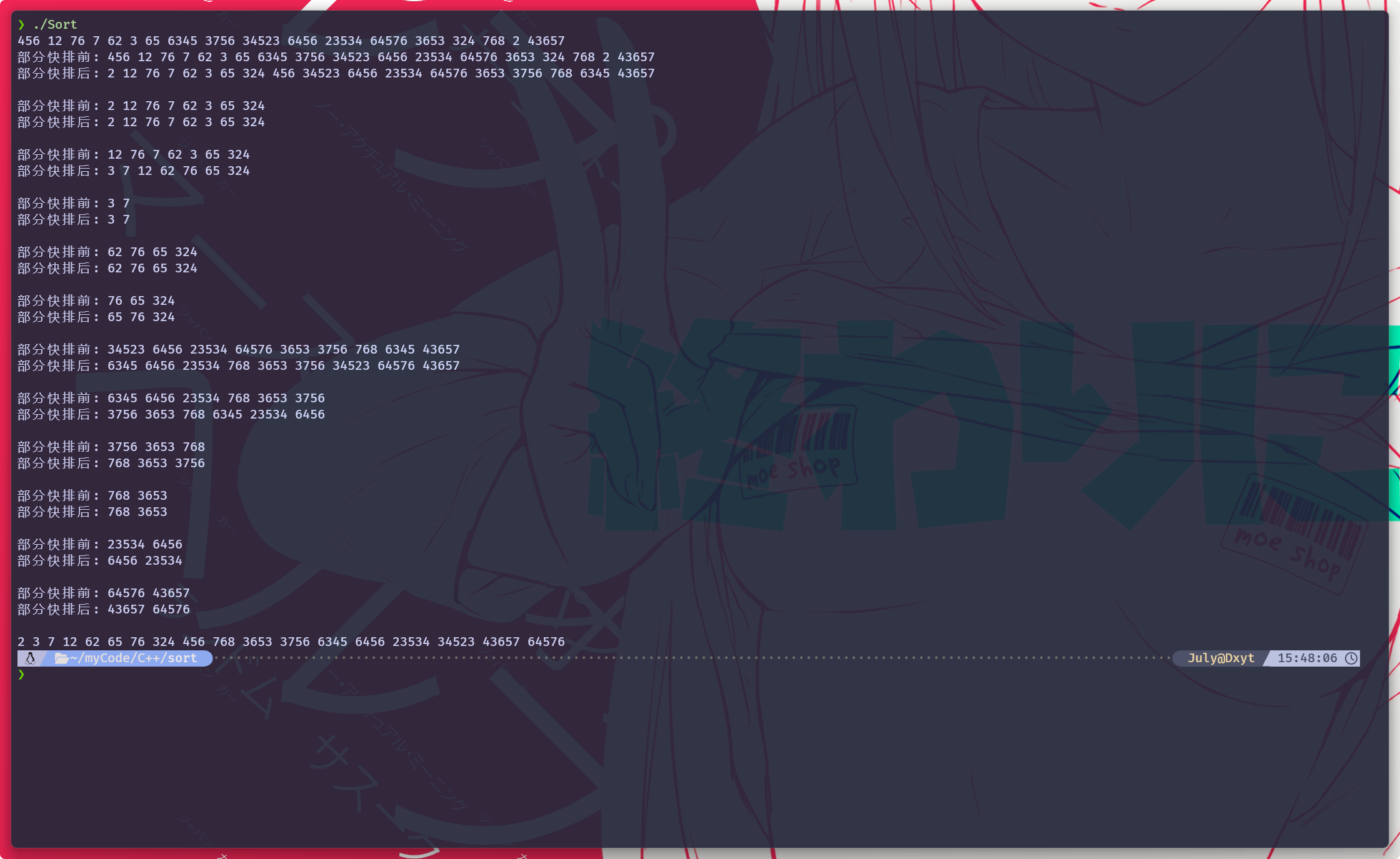
Hoare版有些许不同, 但最终结果是相同的3. 前后指针版
void numSwap(int& num1, int& num2) {
int tmp = num1;
num1 = num2;
num2 = tmp;
}
// 前后指针版
int pointerSortAPart(std::vector<int>& nums, int left, int right) {
int key = nums[left];
int fast = left + 1;
int last = left;
while (fast <= right) {
if (nums[fast] < key && fast != ++last)
numSwap(nums[fast], nums[last]);
fast++;
}
numSwap(nums[left], nums[last]);
return last; // 返回 last, 划分数组界限的位置
}
void _quickSort(std::vector<int>& nums, int begin, int end) {
if (begin >= end) {
return; // 两指针不在维护一个长度>1的有效数组, 返回
}
int keyi = pointerSortAPart(nums, begin, end); // 处理给定范围的数组
_quickSort(nums, begin, keyi - 1); // 处理划分出来 <key的部分
_quickSort(nums, keyi + 1, end); // 处理划分出来 >key的部分
}
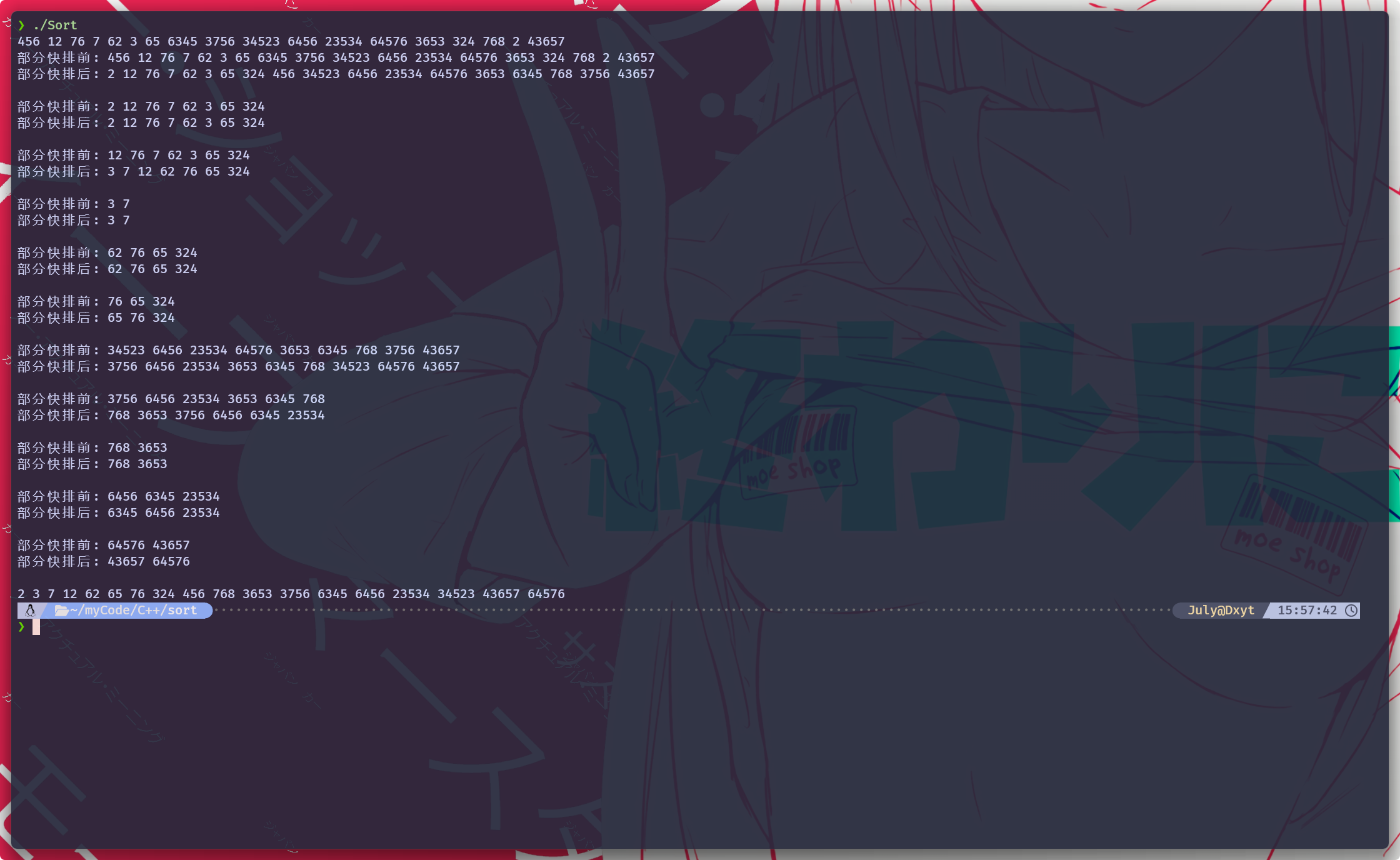
void quickSort(std::vector<int>& nums) {
_quickSort(nums, 0, nums.size()-1);
}
快排优化
key, 将有效范围内的数据分为<=key和>=key的两部分, 对分出的部分, 继续进行相同的操作key的选择是可以影响快排的时间消耗的key, 默认选择首元素, 可能会增加快排的时间消耗key的取值key_quickSort()中进行修改:void numSwap(int& num1, int& num2) {
int tmp = num1;
num1 = num2;
num2 = tmp;
}
int qSortGetMid(std::vector<int>& nums, int begin, int end) {
// 假如 [12, 20], 那么 mid 为 16
int mid = begin + (end - begin) / 2; // begin 不一定为0
if (nums[begin] > nums[mid]) {
if (nums[mid] > nums[end]) // begin > mid > end
return mid;
else if (nums[end] > nums[begin]) // end > begin > mid
return begin;
else
return end;
}
else { // mid > begin
if (nums[end] > nums[mid]) // end > mid > begin
return mid;
else if (nums[begin] > nums[end]) // mid > begin > end
return begin;
else
return end;
}
}
void _quickSort(std::vector<int>& nums, int begin, int end) {
if (begin >= end) {
return; // 两指针不在维护一个长度>1的有效数组, 返回
}
int midi = qSortGetMid(nums, begin, end);
numSwap(nums[midi], nums[begin]); // 将取到的中值, 与数组头元素交换位置, 后边的处理中, 就会用中值做key
int keyi = pointerSortAPart(nums, begin, end); // 处理给定范围的数组
_quickSort(nums, begin, keyi - 1); // 处理划分出来 <key的部分
_quickSort(nums, keyi + 1, end); // 处理划分出来 >key的部分
}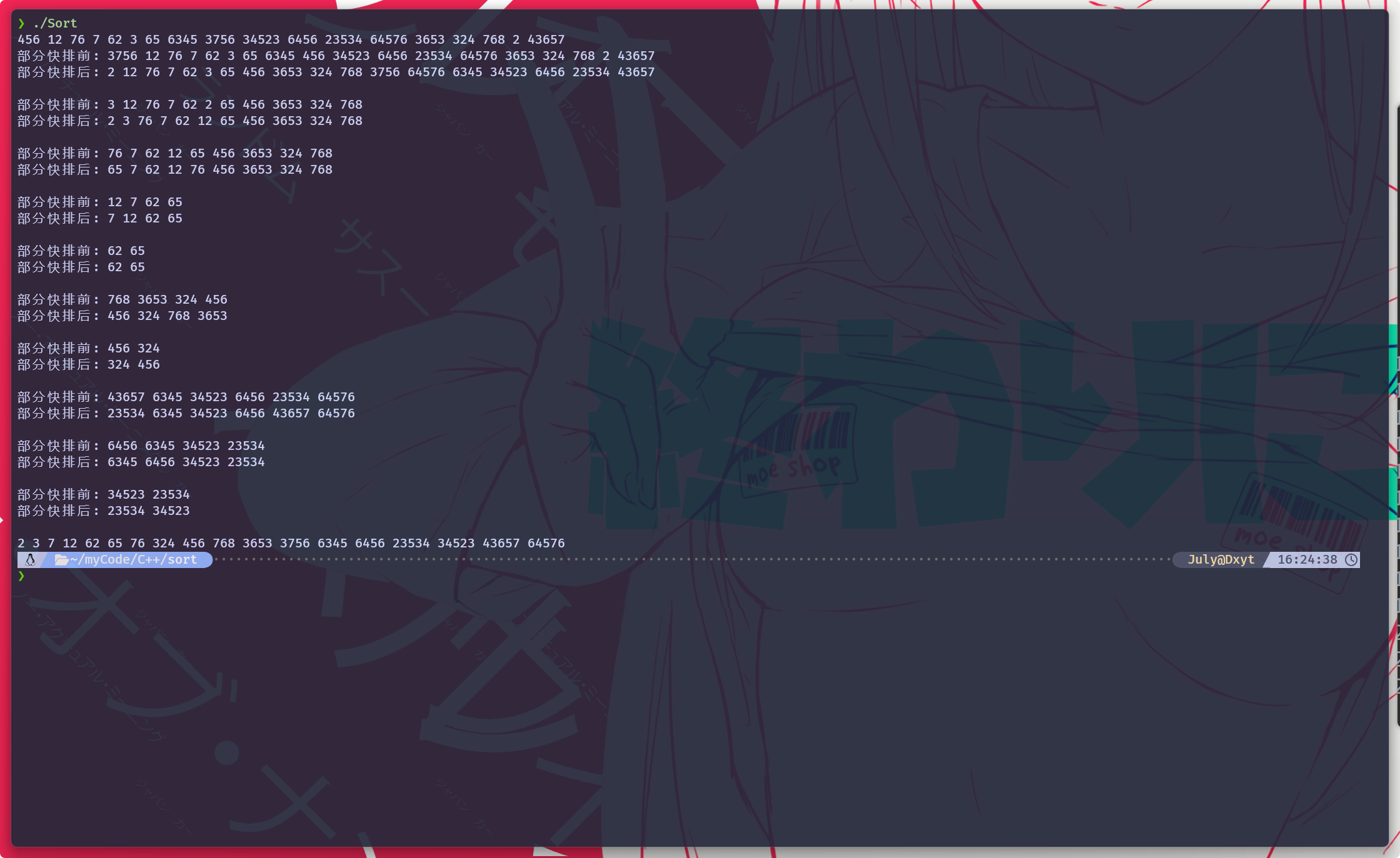
key取值的优化之外, 快排在实际使用时, 还可以进行其他优化非递归快排
hoareSortAPart() pitSortAPart() pointerSortAPart()void nonRecursiveQuickSort(std::vector<int>& nums) {
std::stack<int> qSortIntervalSt; // 快排区间栈, 用于存储数组区间
qSortIntervalSt.push(0);
qSortIntervalSt.push(nums.size() - 1);
while (!qSortIntervalSt.empty()) {
int end = qSortIntervalSt.top();
qSortIntervalSt.pop();
int begin = qSortIntervalSt.top();
qSortIntervalSt.pop();
int midi = qSortGetMid(nums, begin, end);
numSwap(nums[midi], nums[begin]); // 将取到的中值, 与数组头元素交换位置, 后边的处理中, 就会用中值做key
int keyi = pointerSortAPart(nums, begin, end); // 处理给定范围的数组
if (begin < keyi - 1) { // 保证入栈为有效数组区间
qSortIntervalSt.push(begin);
qSortIntervalSt.push(keyi - 1);
}
if (end > keyi + 1) {
qSortIntervalSt.push(keyi + 1);
qSortIntervalSt.push(end);
}
}
}
复杂度
O(N*log N)0和长度为n-1的两部分, 那么 此时时间复杂度就是O(N*N)O(N*log N)O(log N)稳定性
归并排序
逻辑分析
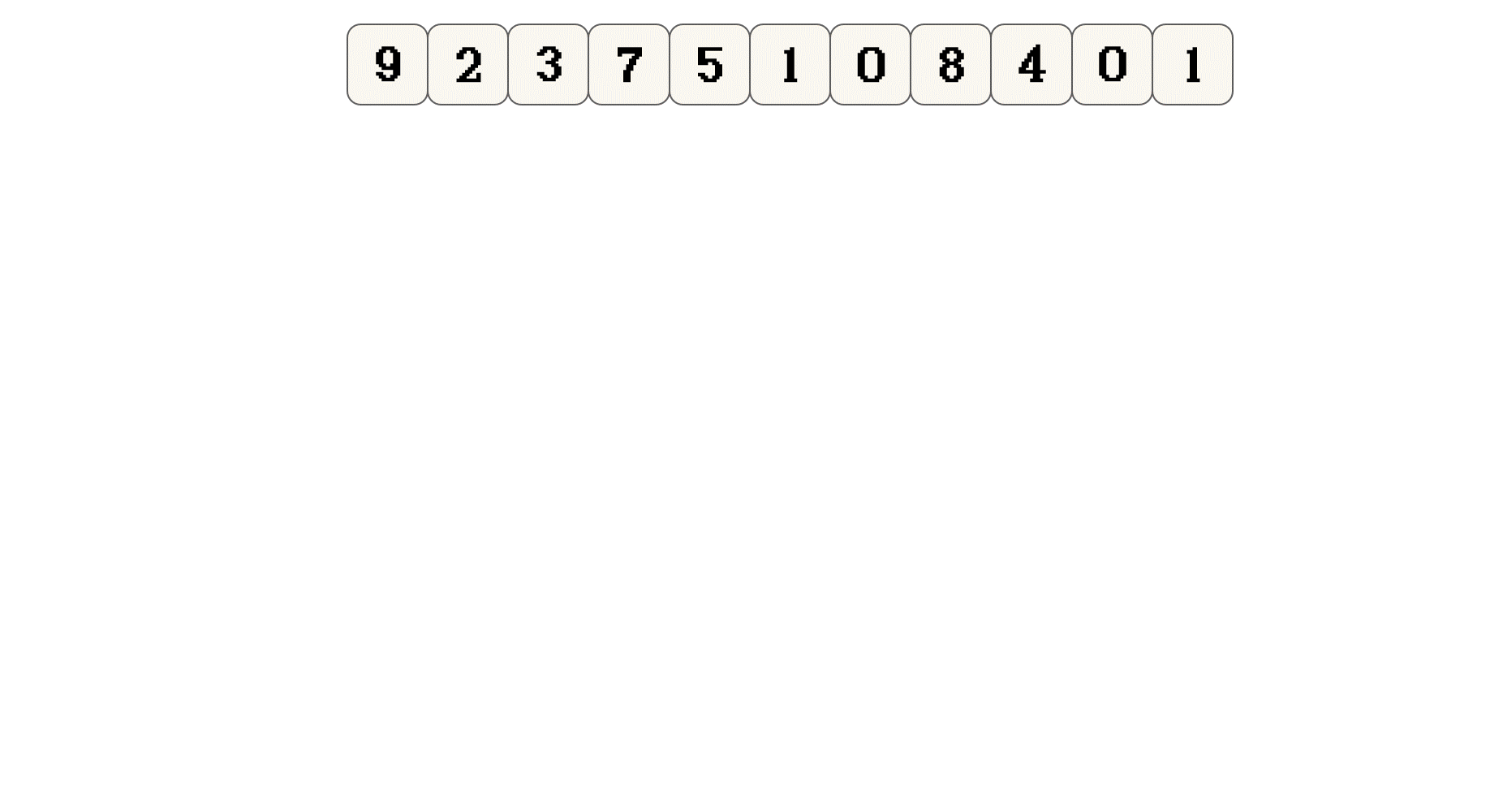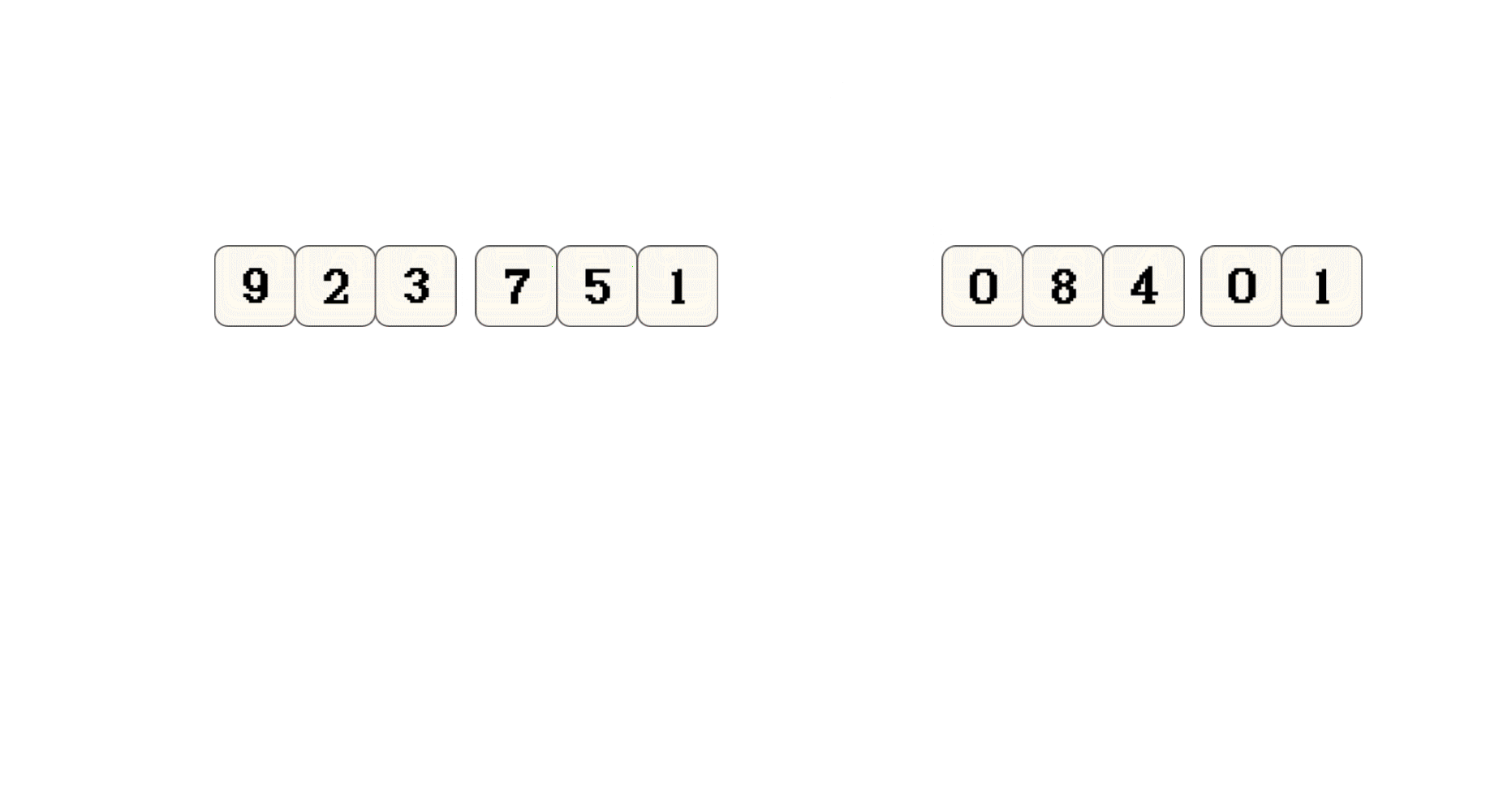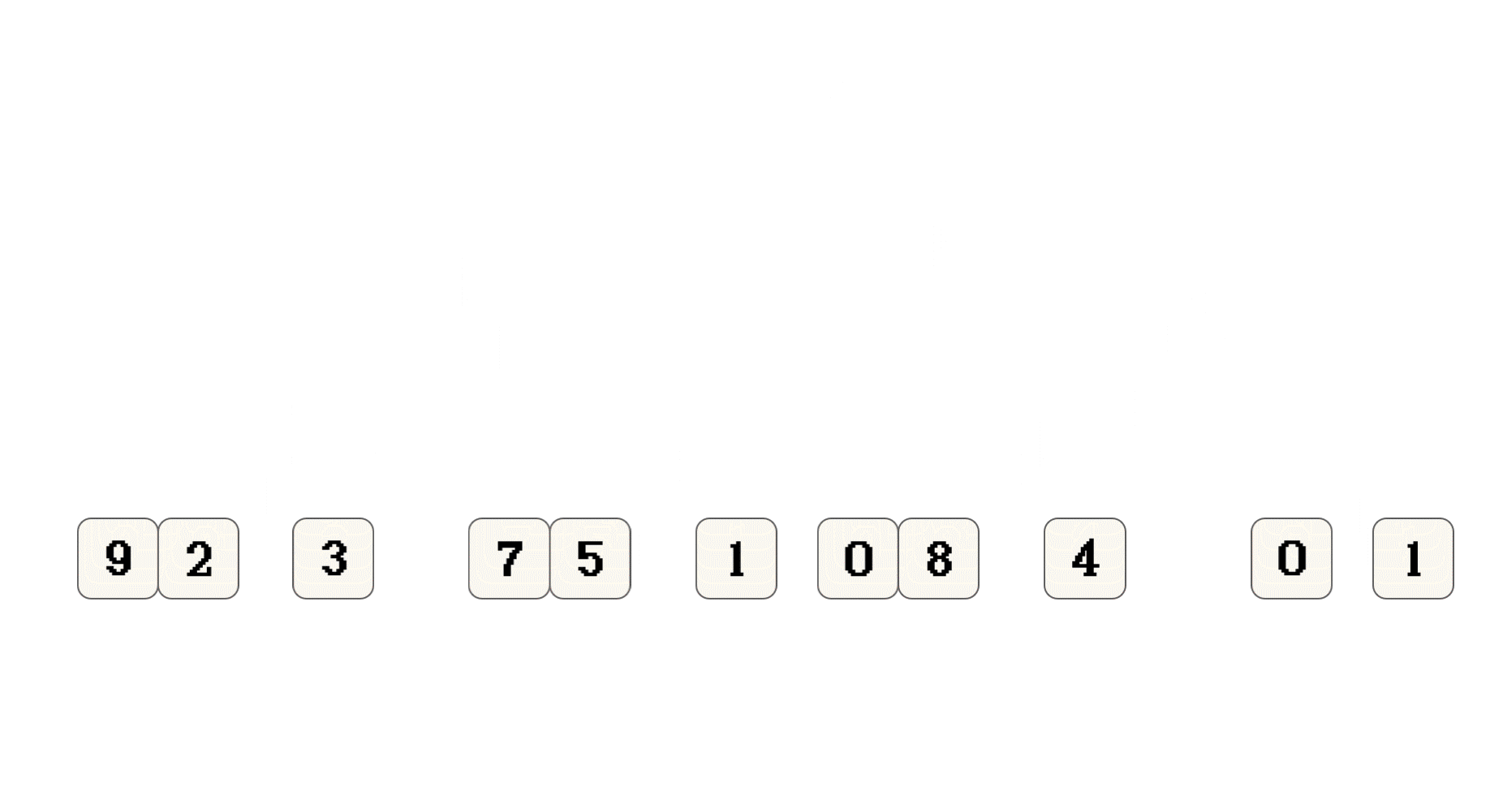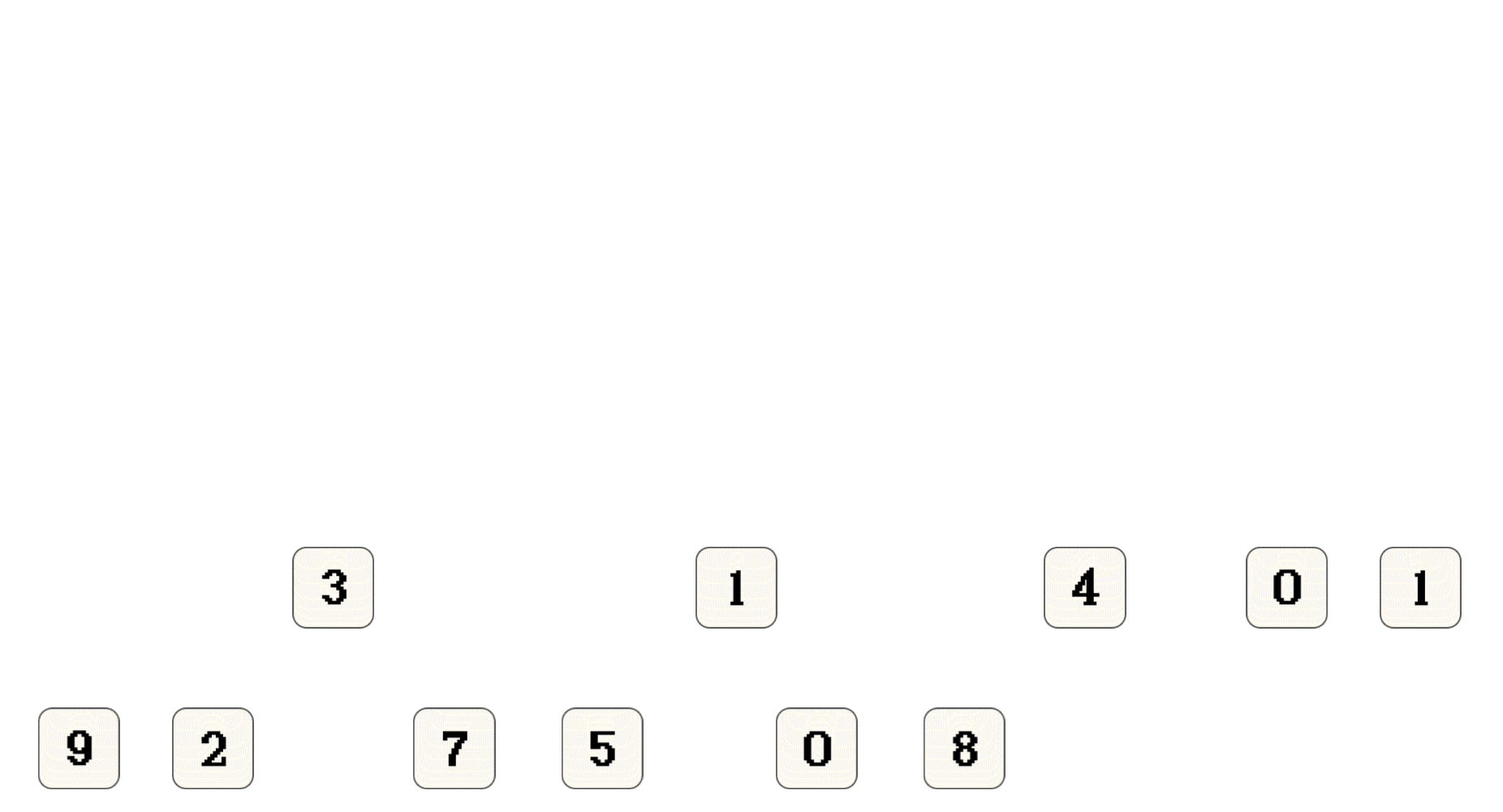
上面只是演示 思想, 并不代表归并排序实际的执行过程
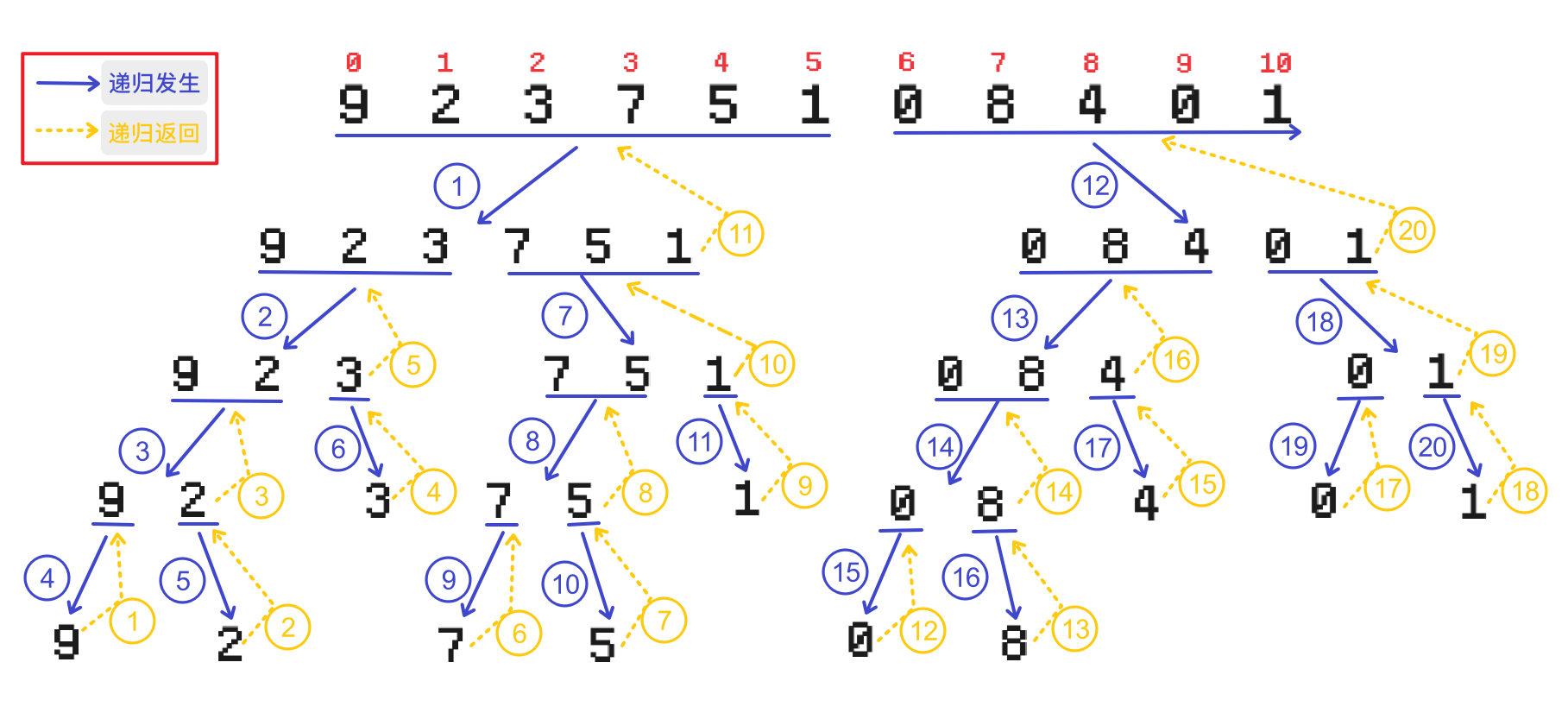
9和2两个子序列进行合并并排序有兴趣可以从图中推算一下, 什么时候会对左右子序列合并
第2次返回之后, 合并
9和2, 结果2 9第4次返回之后, 合并
2 9和3, 结果2 3 9第7次返回之后, 合并
7和5, 结果5 7第9次返回之后, 合并
5 7和1, 结果1 5 7第10次返回之后, 合并
2 3 9和1 5 7, 结果1 2 3 5 7 9第13次返回之后, 合并
0和8, 结果0 8第15次返回之后, 合并
0 8和4, 结果0 4 8第18次返回之后, 合并
0和1, 结果0 1第19次返回之后, 合并
0 4 8和0 1, 结果0 0 1 4 8第20次返回之后, 合并
1 2 3 5 7 9和0 0 1 4 8, 结果0 0 1 1 2 3 4 5 7 8 9
代码实现
// 归并 排序的递归函数
void _mergeSort(std::vector<int>& nums, int begin, int end, std::vector<int>& tmpNums) {
// 如果begin和end维护的序列长度 <=1, 返回
if (begin >= end)
return;
// 计算中间位置
int mid = (begin + end) / 2;
// 开始递归分化
_mergeSort(nums, begin, mid, tmpNums); // 先左子序列
_mergeSort(nums, mid + 1, end, tmpNums); // 再右子序列
// 走到这里, 表示begin~mid 和 mid+1~end, 两序列在原数组中有序
// 需要将这两部分进行合并, 不能直接在原数组中合并, 会覆盖还没有处理的数据
// 在tmpNums中合并, 再拷贝到原数组对应位置
int beginLeft = begin, endLeft = mid; // 左子序列的开始和结束位置
int beginRight = mid + 1, endRight = end; // 右子序列的开始和结束位置
// 遍历两个序列, 直到一个序列遍历结束
while (beginLeft <= endLeft && beginRight <= endRight) {
if (nums[beginLeft] <= nums[beginRight])
tmpNums.push_back(nums[beginLeft++]);
else
tmpNums.push_back(nums[beginRight++]);
}
// 走到这里, 至少有一个序列的所有数据都已经存储到了tmpNums
// 可能还有另外一个序列没有遍历结束
while (beginLeft <= endLeft) {
tmpNums.push_back(nums[beginLeft++]);
}
while (beginRight <= endRight) {
tmpNums.push_back(nums[beginRight++]);
}
// 走到这里, 两个子序列已经合并在tmpNums中并有序
// 再将tmpNums的数据, 按照对应位置映射到nums的begin~end中
int tmpBegin = begin;
while (begin <= end) {
nums[begin++] = tmpNums[begin - tmpBegin];
// 赋值, 左表达式后执行, 所以可以++
}
// 清空tmpNums
tmpNums.resize(0);
}
void mergeSort(std::vector<int>& nums) {
// 归并排序需要合并数组, 所以要用一个临时数组
// 但是如果每次递归时, 都创建一个临时数组, 会有额外开销, 所以在开始递归之前, 定义一个数组
// 向递归函数传入数组就可以了
std::vector<int> tmpNums;
_mergeSort(nums, 0, nums.size() - 1, tmpNums);
}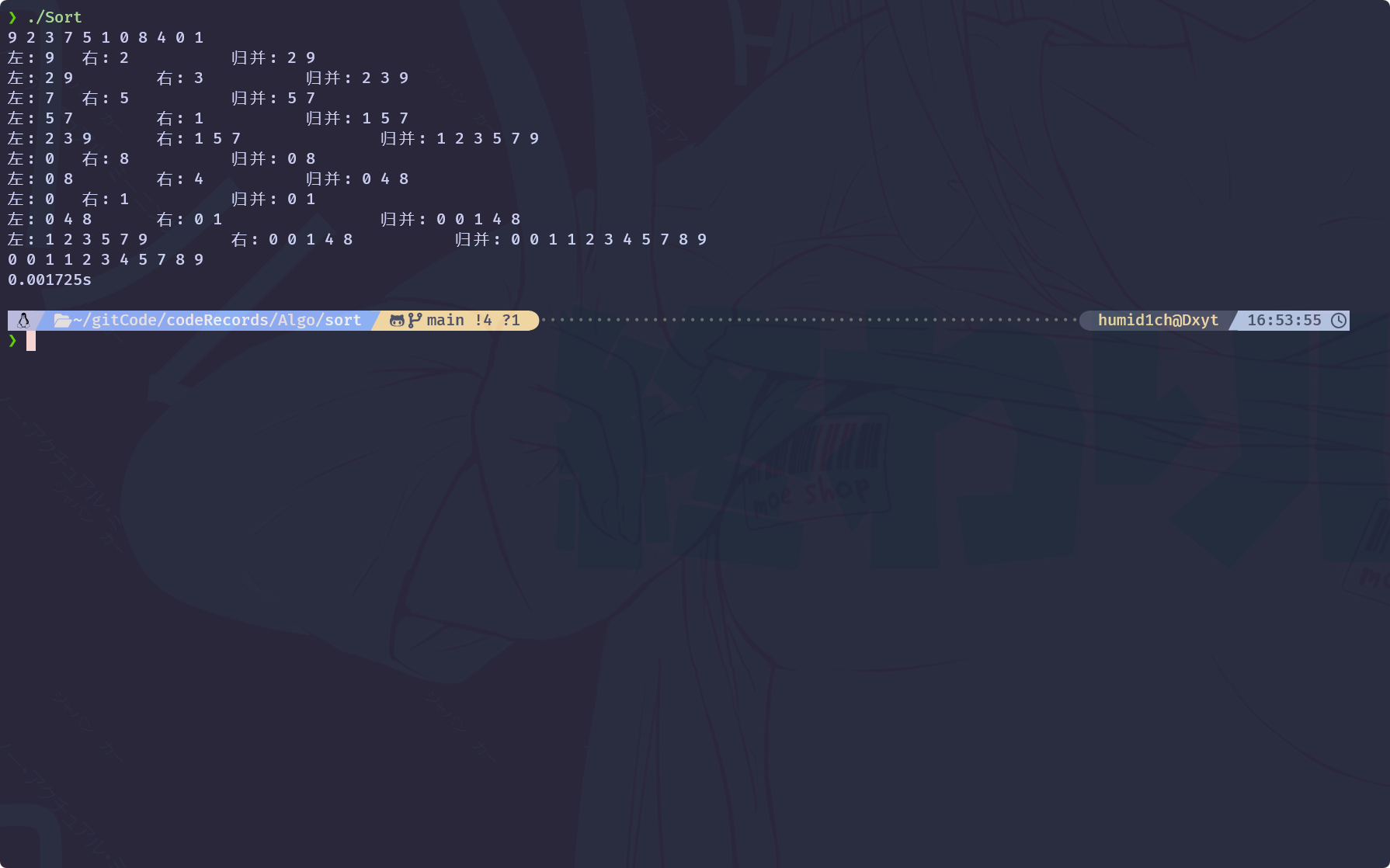
非递归实现
- 一一分组, 区间归并
- 两两分组, 区间归并
- 四四分组, 区间归并
- 八八分组, 区间归并
- …
void nonRecursiveMergeSort(std::vector<int>& nums) {
std::vector<int> tmpNums;
int gap = 1;
// 从间隔为1开始, 对间隔区间内的数据进行归并
while (gap < nums.size()) {
for (int i = 0; i < nums.size(); i += gap * 2) {
int beginLeft = i, endLeft = i + gap - 1; // g = 1, 0 0, 2 2
int beginRight = i + gap, endRight = i + 2 * gap - 1; // g = 1, 1 1, 3 3
// 因为是以固定的间隔规律进行 区间划分的, 所以要判断一下, 区间是否在数组内
// 首先, beginLeft 不会越界, 因为以i赋值
// 所以要判断其他三个
if (endLeft >= nums.size())
endLeft = nums.size() - 1;
if (beginRight >= nums.size()) // 第二个区间不存在
endRight = nums.size() - 1;
else if (endRight >= nums.size())
endRight = nums.size() - 1;
// 开始归并 [beginLeft, endLeft] 和 [beginRight, endRight]
while (beginLeft <= endLeft && beginRight <= endRight) {
if (nums[beginLeft] < nums[beginRight])
tmpNums.push_back(nums[beginLeft++]);
else
tmpNums.push_back(nums[beginRight++]);
}
while (beginLeft <= endLeft) {
tmpNums.push_back(nums[beginLeft++]);
}
while (beginRight <= endRight) {
tmpNums.push_back(nums[beginRight++]);
}
}
// 退出for循环, 则表示以gap为间隔进行划分区间, 并对区间两两归并完毕
// 向原数组中赋值
nums.swap(tmpNums);
tmpNums.resize(0);
gap *= 2; // 扩大间隔, 扩大下次划分区间的间隔
}
}
复杂度
O(N)O(N)O(N*log N)稳定性
计数排序
逻辑分析
nums, 映射计数数组countnums[i] = 1, 那么就可以将nums[i]映射到count[1]位置nums[i] = 10, 那么就可以将nums[i]映射到count[10]位置nums数组的值 作为count数组的下标nums中的所有数据按照这样的思路在count中之后, 遍历count, 其实就可以按照数据大小的先后顺序遍历所有数据count的过程中, 将数据在按照顺序放入nums数组中, 就可以实现队员数组的内容进行排序count中对应数据的映射位置也不会存储原数据, 而是记录映射数据的个数count时, 就可以将原数组中相同的数据一起放入nums中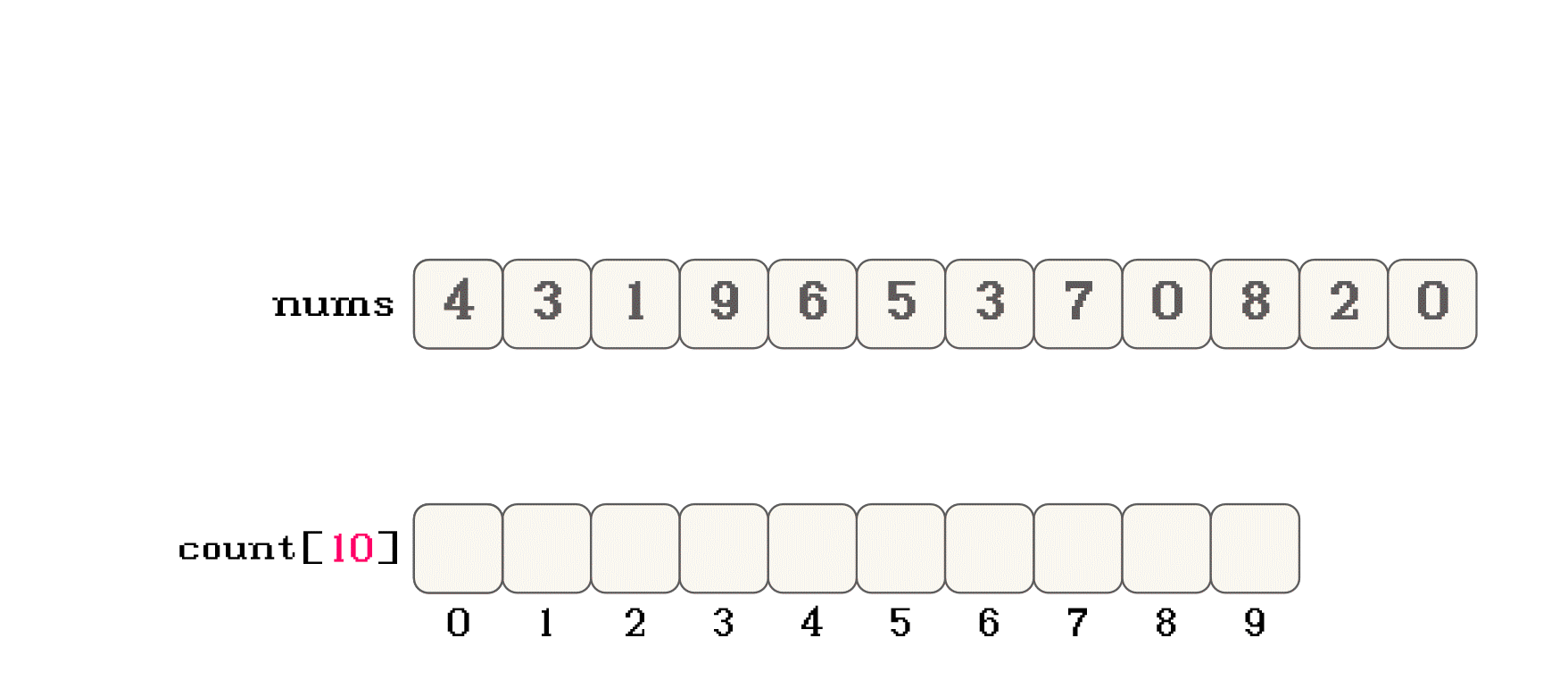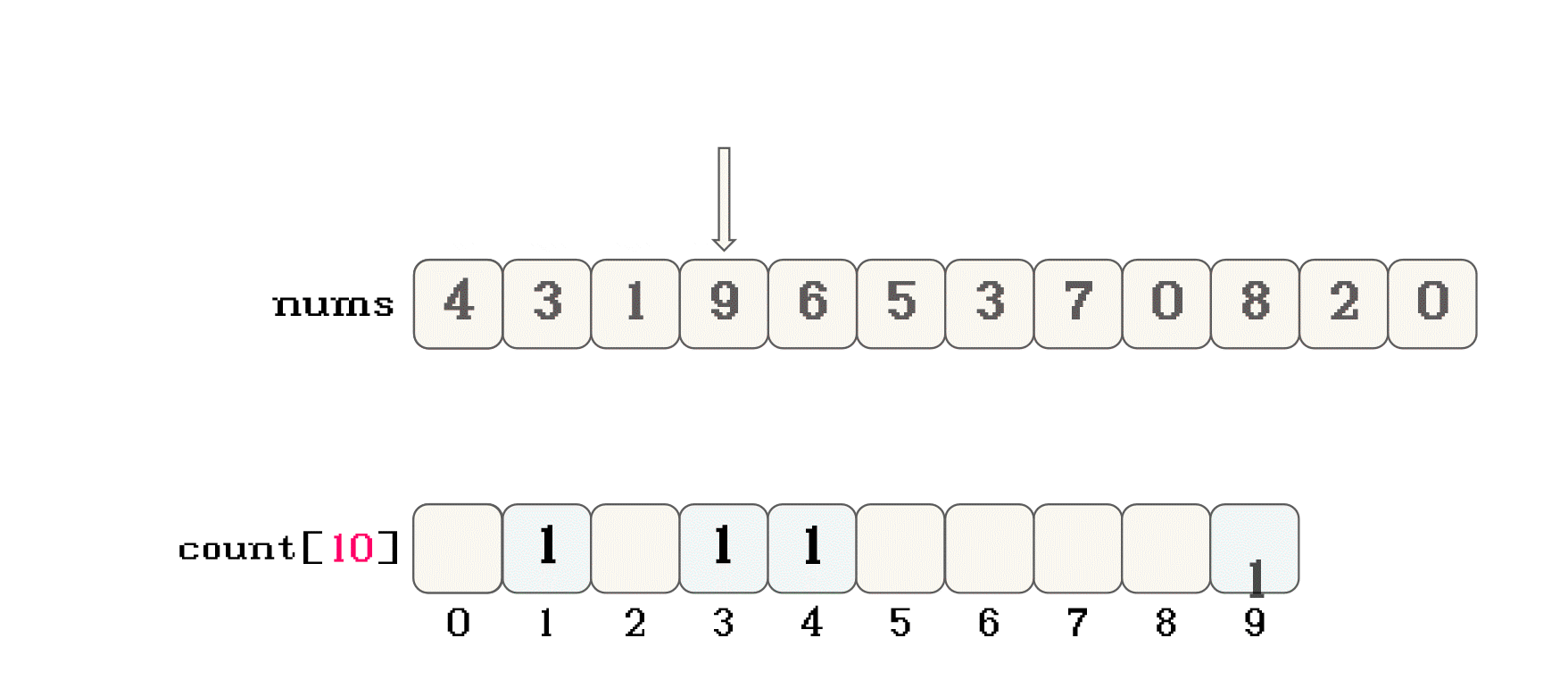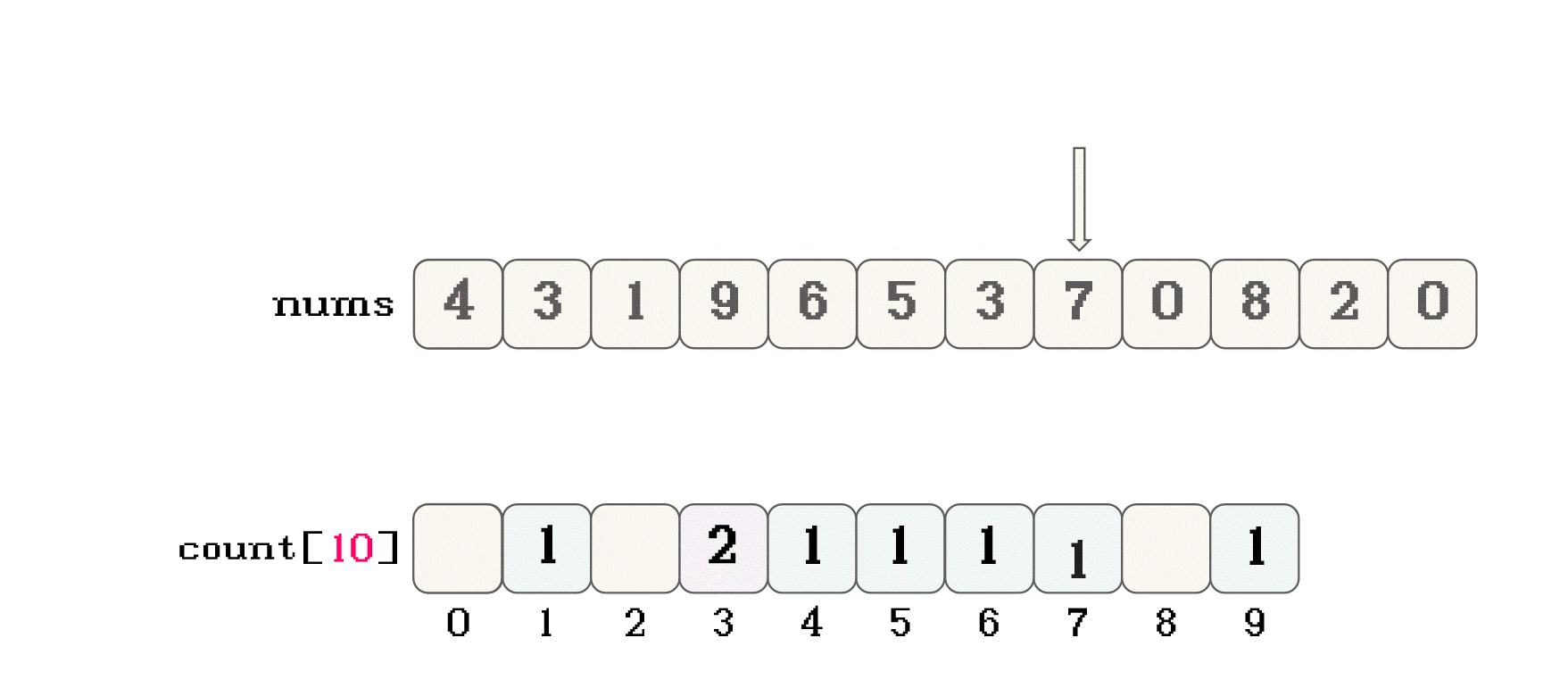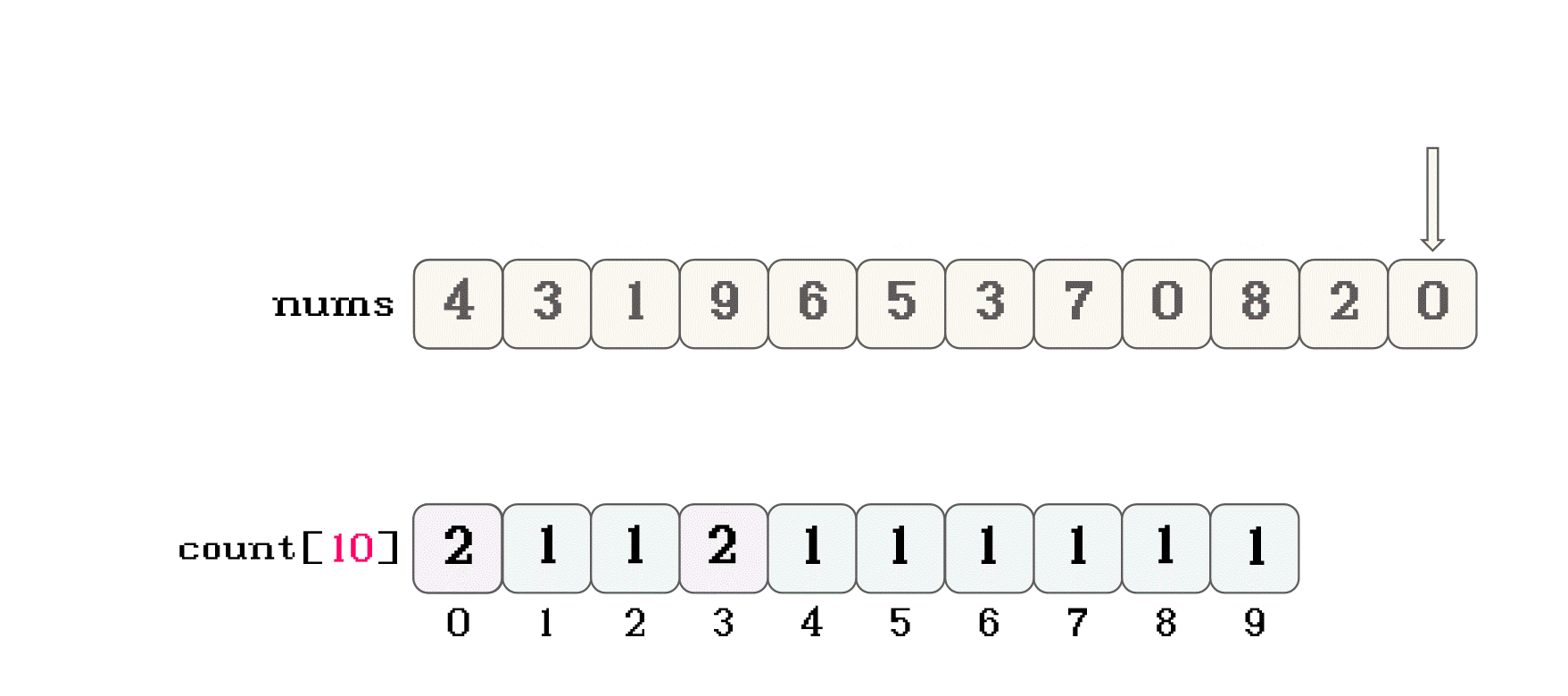
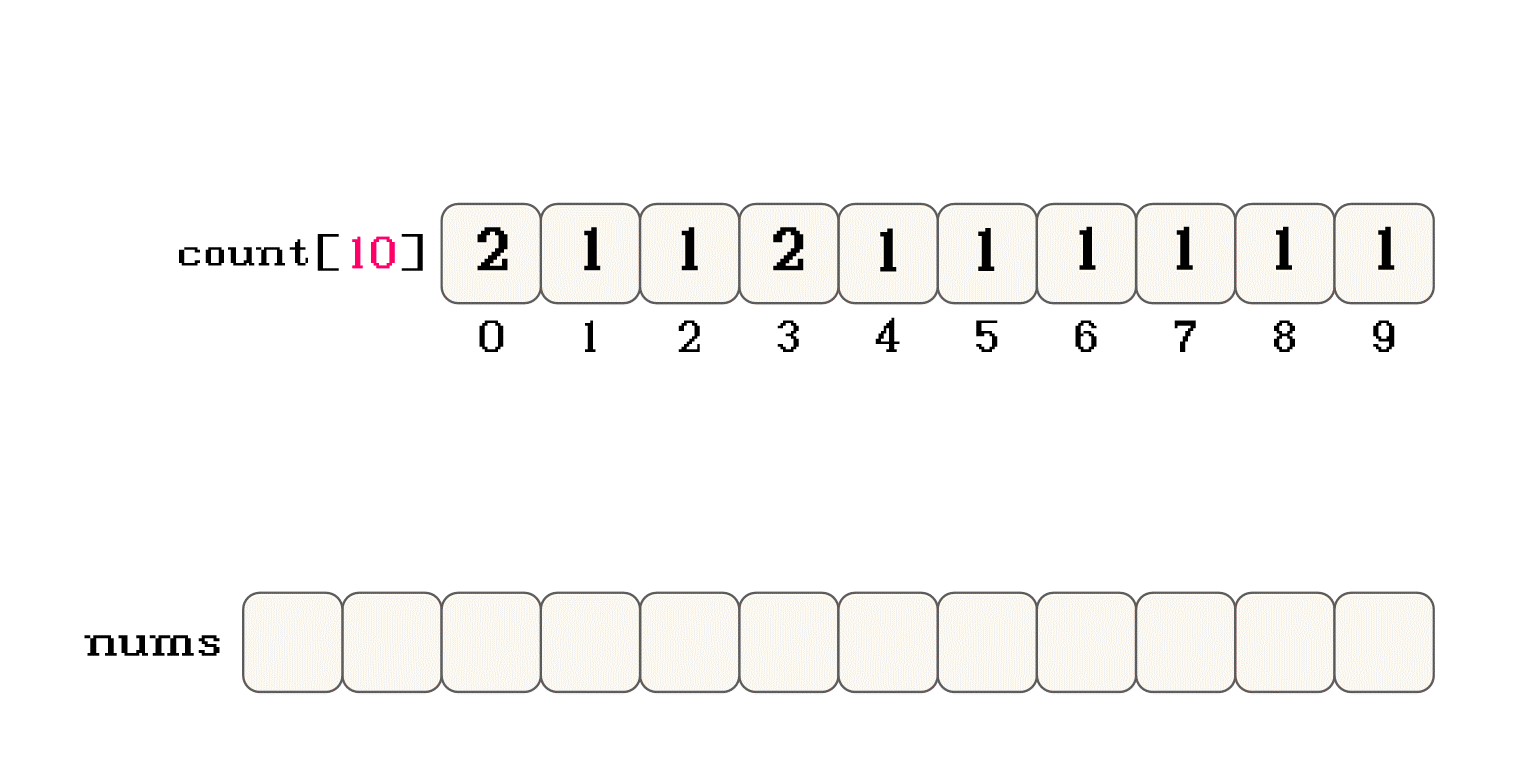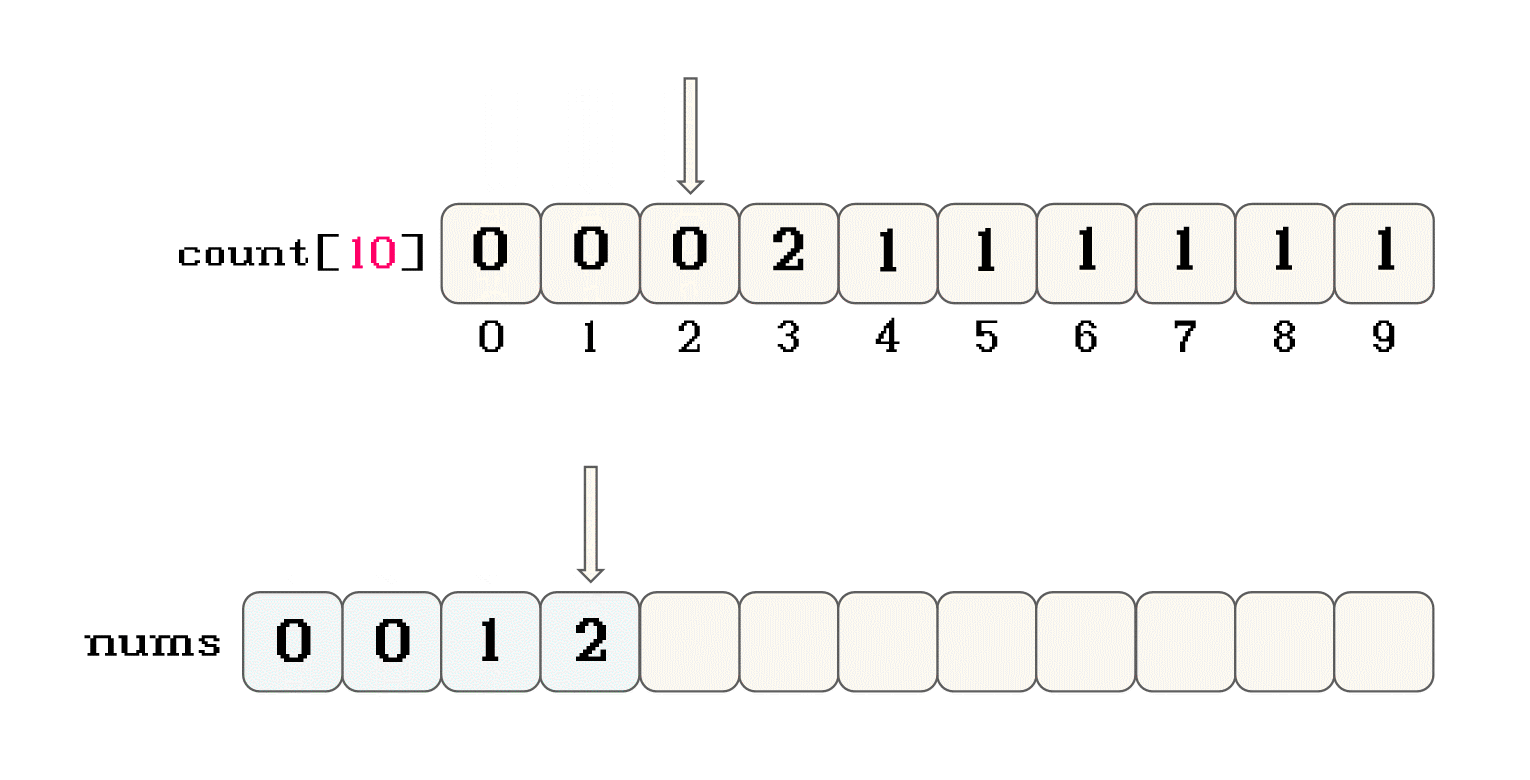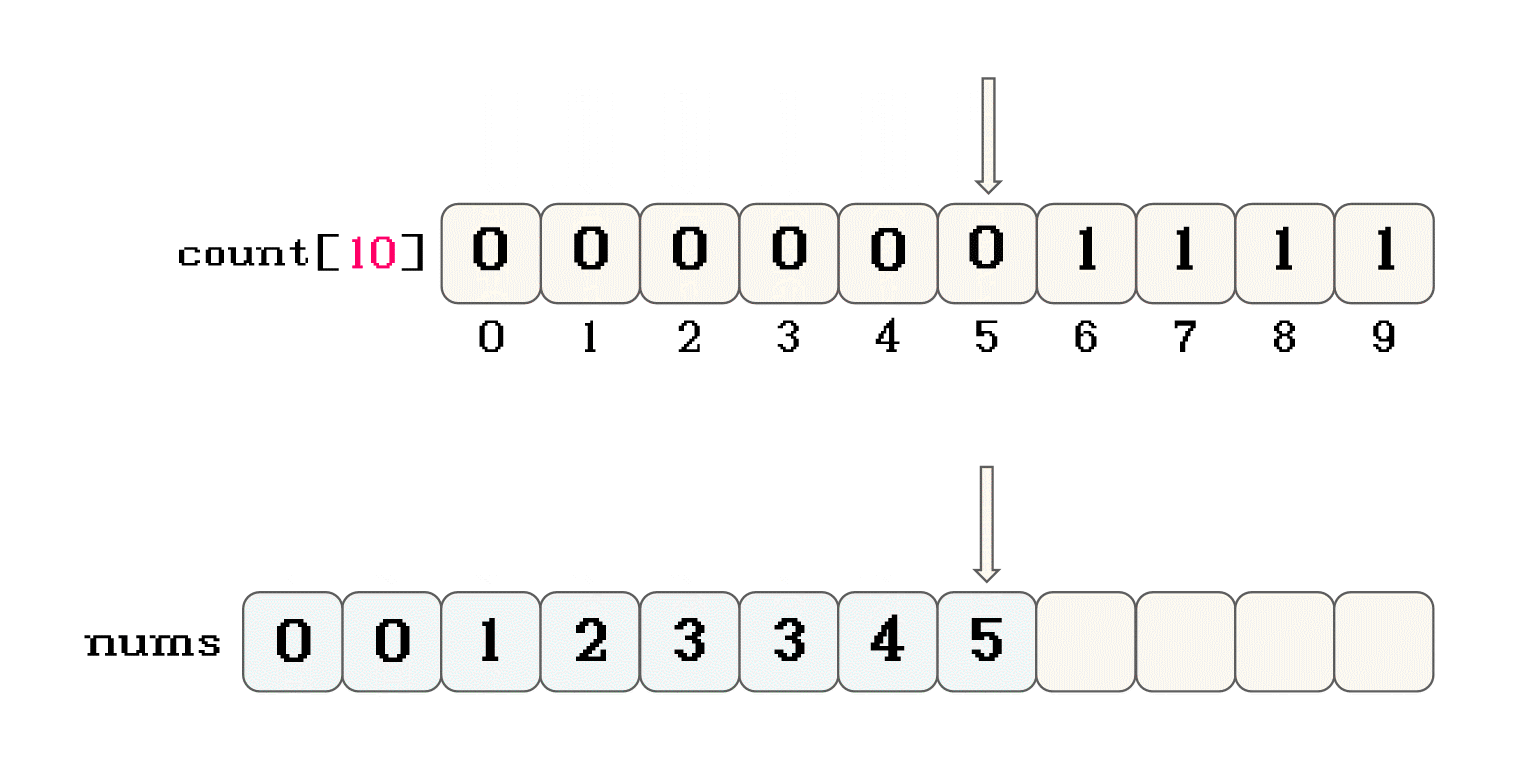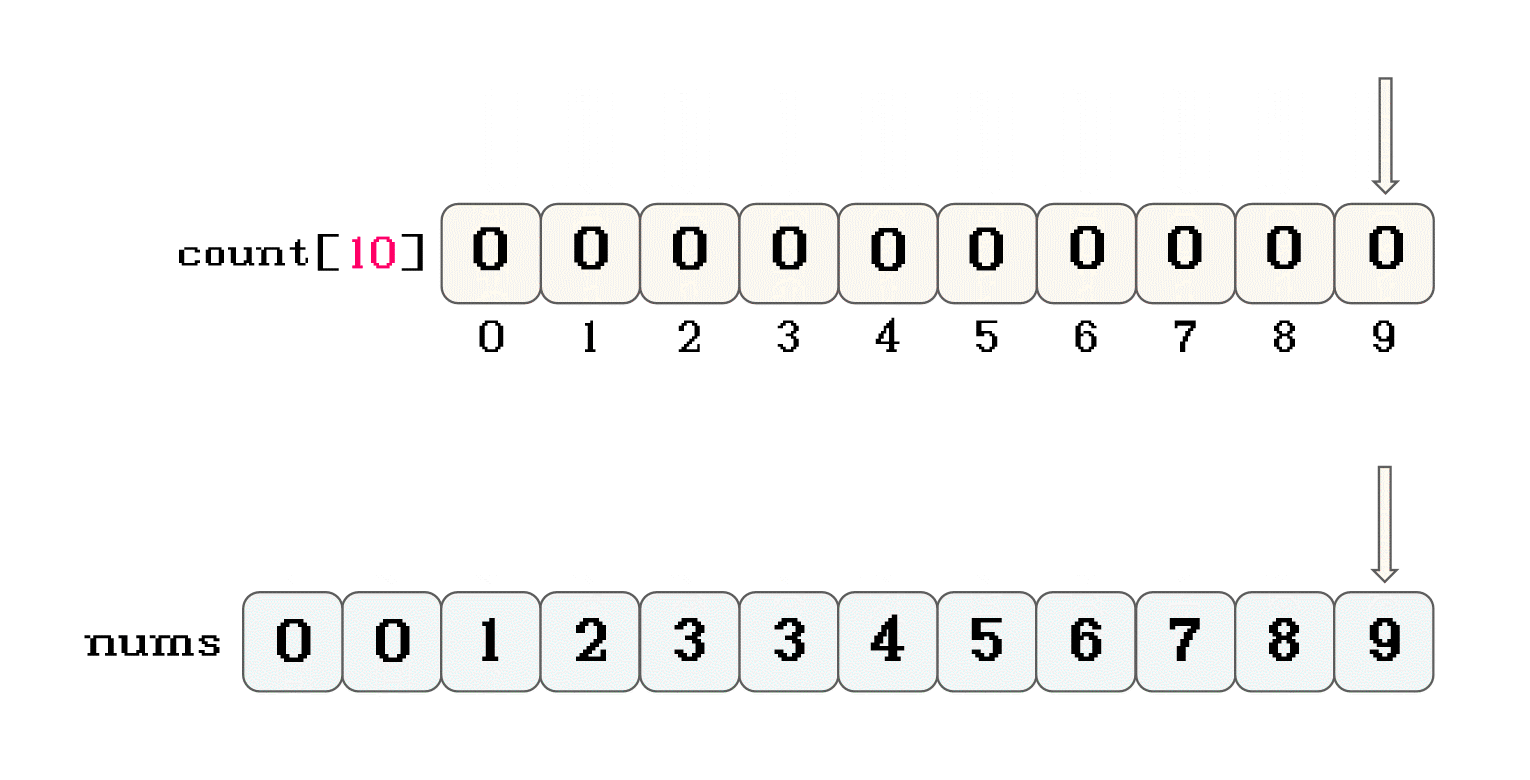
nums中赋值的规则是什么?nums中赋值的过程就是排序的过程-
遍历映射数组
-
如果
count[n] > 0, 就将n放置在原数组中, 同时count[n]--在原数组中放置数据的过程中, 在原数据中位置是从
0开始的, 每放置一个数据位置向后移 -
直到映射数组中的所有元素都为
0, 可以看作数据全部按大小顺序还原到原数组中
代码实现
count开辟为max(nums)的大小, 那么count数组中min(nums)位置之前的空间就都被浪费了, 因为不会有数据放在其中min(nums)映射在count[0]count的大小应该是max-min+1, 映射时, 也应该对 数据-min进行映射, 还原时也应该+minvoid countSort(std::vector<int>& nums) {
// 找nums中的最大值和最小值
int max = nums[0], min = nums[0];
for (auto e : nums) {
if (e > max)
max = e;
if (e < min)
min = e;
}
std::vector<int> count(max - min + 1); // 构建count数组
for (int i = 0; i < nums.size(); i++) {
count[nums[i] - min]++; // 映射并计数
}
int j = 0;
for (int i = 0; i < count.size(); i++) {
while (count[i]-- > 0) { // 将count[i]清零
nums[j++] = i + min;
}
}
}
复杂度
max-min <= nums.size(), 那么就是O(N), 否则就是O(max-min)2和64576, 差值为64574, 那么在排序时 遍历count数组, 循环就需要执行6w多次, 而实际上nums.size()才186w多次的循环, 比18的3次方的十倍还要多O(max-min)稳定性
count数组中计数的6 6 6 6 6, 那么count[6]最终值就等于56, 即count[6]==5时, 表示的是最后一个6堆排序
逻辑分析
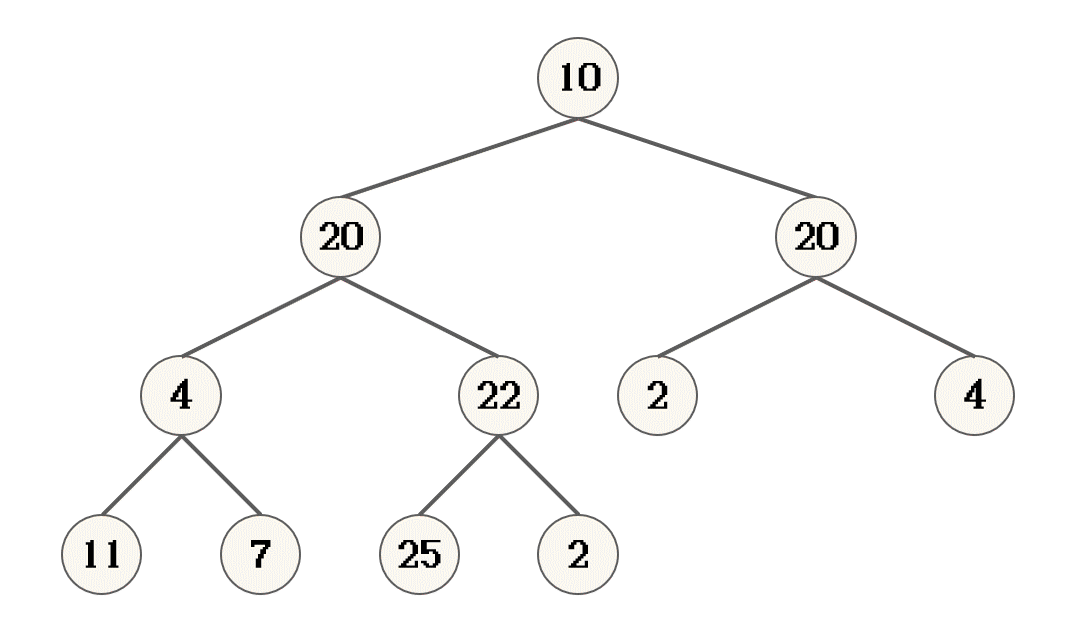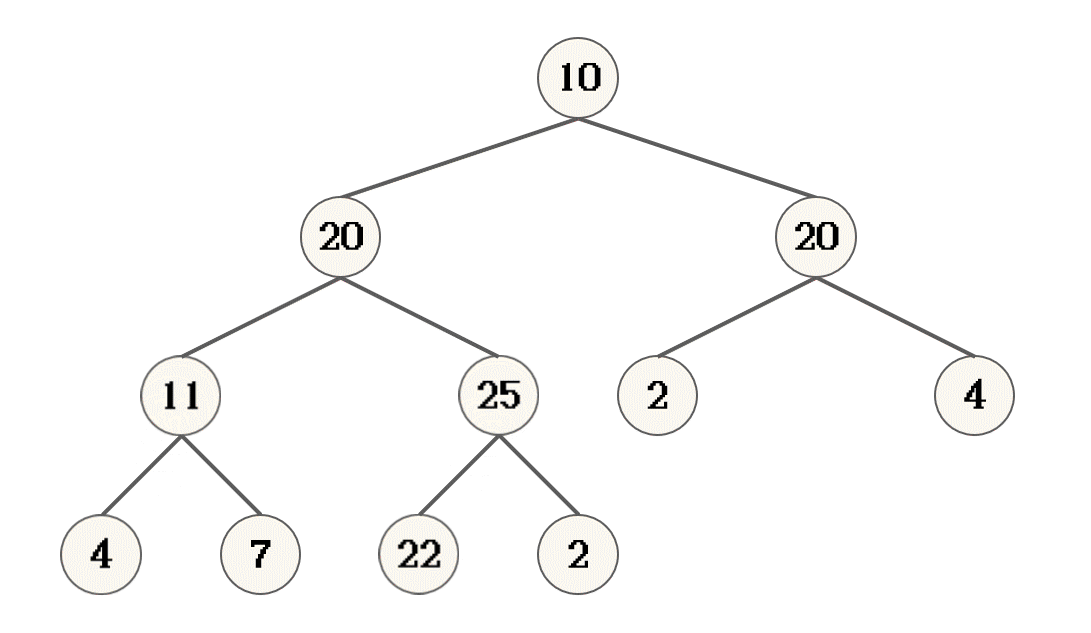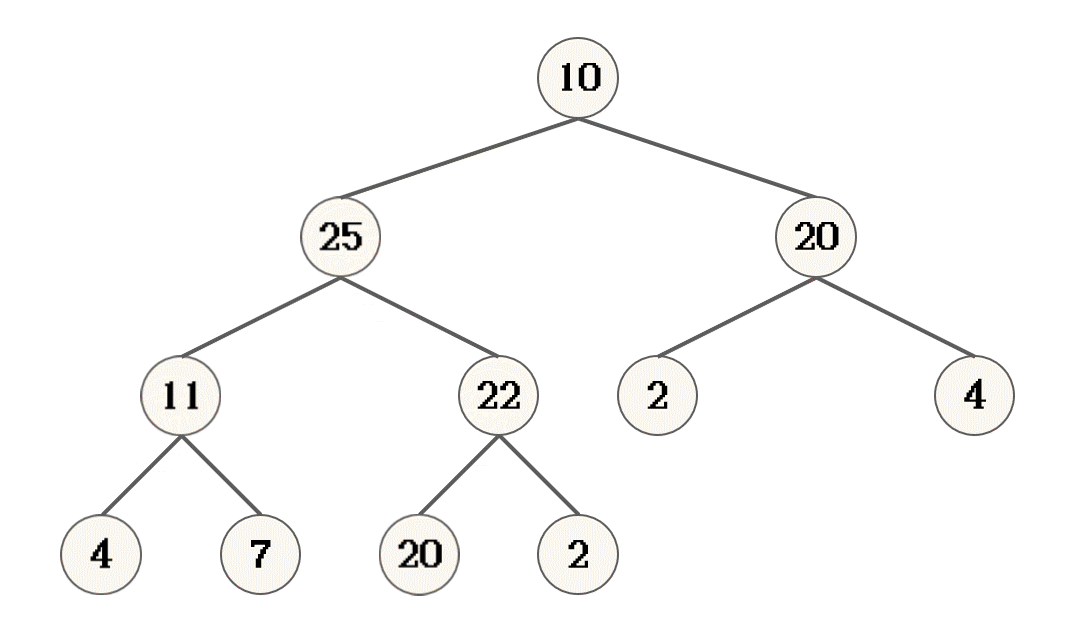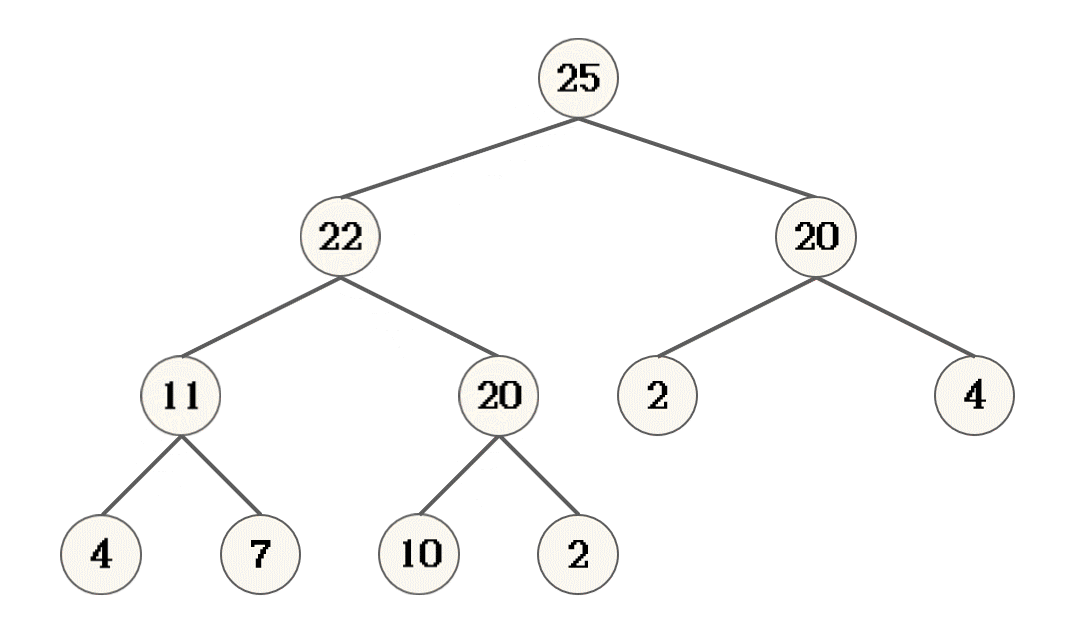
- 提供一棵树的根, 如果此树拥有子节点, 根记录为父节点, 其左右子节点的较大节点记录为子节点
- 对比父节点与字节点的大小, 如果子节点大, 则父子结点交换位置
- 交换完成之后, 父节点的新位置, 记录做新的父节点
- 将新的父节点, 当作一棵树的根, 重复上面的操作, 直到新的父节点不存在子节点
- 此时, 完成向下调整
10节点的左子节点20作为一个树的根 进行向下调整时, 20节点的两颗子树已经是大根堆了- 叶子节点, 不存在子节点, 不需要调整
- 对完全二叉树来说, 最后一个非叶子节点 的子节点, 必定是叶子节点, 也就表示最后一个非叶子节点的子树可以看作是一个大根堆
22节点就是最后一个非叶子节点[10, 20, 20, 4, 22, 2, 4, 11, 7, 25, 2]
2 * i + 1, 右孩子: 2 * i + 2size / 2 - 1和(size + 1) / 2 - 1的结果是相同的, 都是其父亲节点的下标size / 2 - 1 表示只有左孩子时, 根据size计算父节点下标(size + 1) / 2 - 1就可以表示有右孩子时, 根据有左孩子时的size计算父节点下标size / 2 - 1计算父节点的下标代码实现
void numSwap(int& num1, int& num2) {
int tmp = num1;
num1 = num2;
num2 = tmp;
}
// 建立大根堆 向下调整 函数
void bigRootAdjustDown(std::vector<int>& nums, int size, int root) {
// 传入数组 和 数组下标作为需要调整的树的根节点
// 另外这里传入的size不代表数组的总长度, 而是 可以看作是完全二叉树的数据的长度
// 也就是 size 之后的数据, 不需要调整
// 要处理的数据范围是[0, size)
// 记录 parent 和 child(左孩子节点, 因为右孩子不一定存在)
// 根据完全二叉树的特点, 计算一个节点的左孩子节点下标
int parent = root;
int child = parent * 2 + 1;
while (child < size) {
// child 默认表示左孩子, 要判断左右孩子谁大
if (child + 1 < size && nums[child] < nums[child + 1])
child++; // 右孩子大, child += 1 记录右孩子下标
if (nums[parent] < nums[child]) {
numSwap(nums[parent], nums[child]);
parent = child;
child = parent * 2 + 1;
}
else { // 已经是大根堆了
break; // 不需要再向下走, 此次调整完毕
}
}
}
void heapSort(std::vector<int>& nums) {
// 先建立 大根堆
// 从最后一个非叶子节点开始
for (int index = nums.size() / 2 - 1; index >= 0; index--) {
bigRootAdjustDown(nums, nums.size(), index);
}
// 大根堆建立完成
// 正式开始堆排序
// 进入循环之前, 数组首元素已经是最大值, 所以先将首元素与尾元素调换位置
// 并缩减需要 向下调整处理的数据范围
// 直到 缩减到 0
int end = nums.size() - 1; // 需要处理的数据范围 [0, end)
while (end > 0) {
numSwap(nums[end], nums[0]);
bigRootAdjustDown(nums, end, 0);
end--; // 缩减end
}
// 排序完毕
}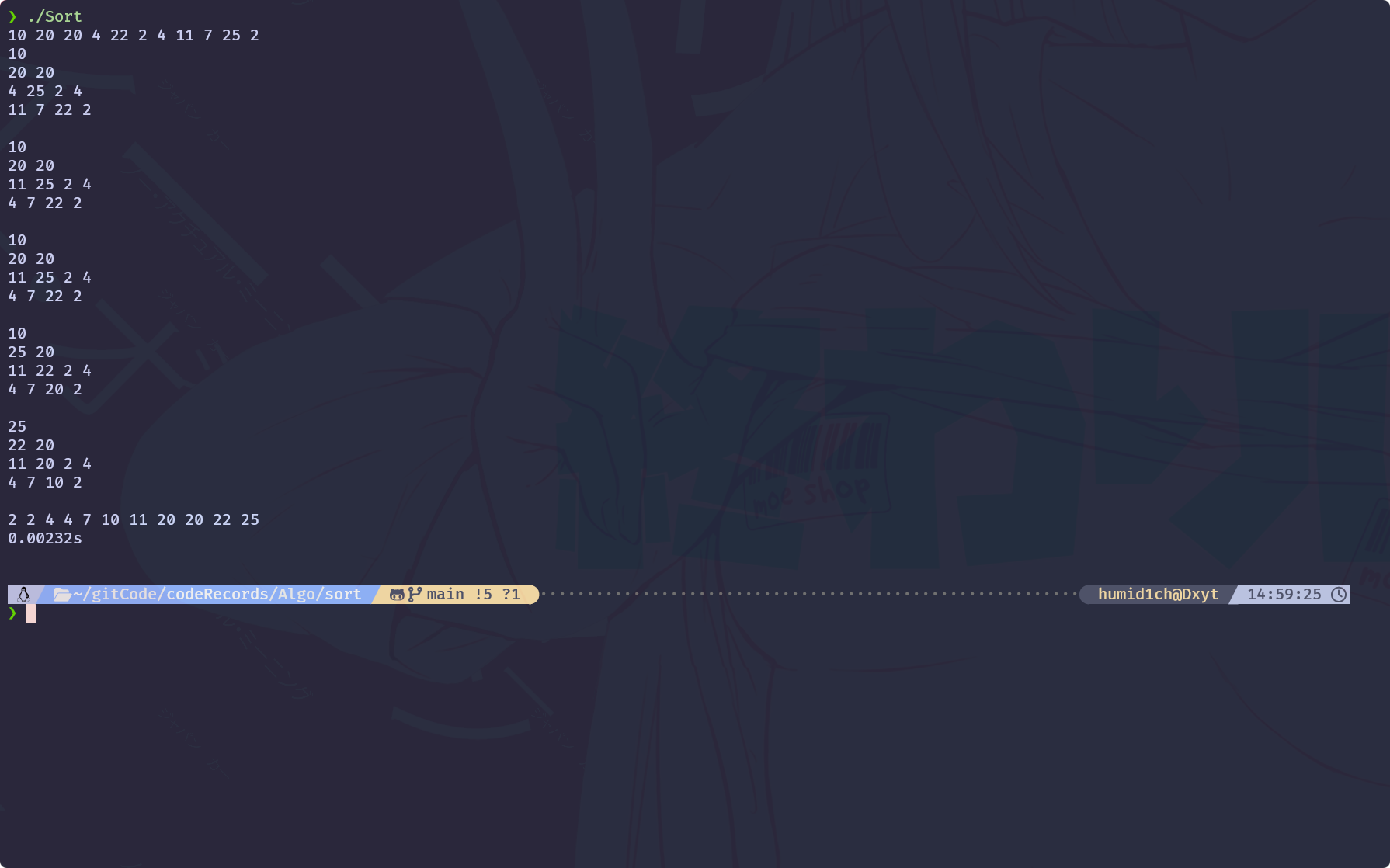
复杂度
O(1)稳定性
作者: 哈米d1ch 发表日期:2024 年 8 月 3 日