
算法
2024 年 8 月 1 日
[算法] 八大排序I: 冒泡、选择、插入、希尔排序 的逻辑、复杂度、稳定性详解 - C++实现
前情提要
本文章所有排序方法, 默认按照升序分析
八大排序: 冒泡排序, 选择排序, 插入排序, 希尔排序, 快速排序, 堆排序, 归并排序, 计数排序
但是, 这8种排序方法, 不一定只有一种实现方法, 不同的实现方式也会存在差异
本篇文章的排序测试结果的截图, 均已一定的规则进行函数调用
但文章中的代码实现, 只实现排序部分, 不实现打印提示与数据
测试时的函数调用规则如下:
排序函数内部, 打印开始与结束的提示, 例:
void bubbleSort() { cout << "冒泡排序开始" << endl << endl; /* 冒泡排序主体 */ cout << "冒泡排序结束" << endl; }每趟排序完成之后, 打印排序趟数以及本趟排序完成之后的结果:
// 数组打印函数, 在有需要时直接调用 void printVector(const std::vector<int>& nums) { for (auto elem : nums) { cout << elem << " "; } cout << endl; } void printVector(const std::vector<int>& nums, int begin, int end) { for (int i = begin; i <= end; i++) { cout << nums[i] << " "; } }
冒泡排序
逻辑分析
冒泡排序, 可以从命名上大概了解排序的逻辑
冒泡排序的大概逻辑就是, 每趟循环 从数组头遍历到数组尾, 同时将遍历过程中遇到的最大值或最小值向数组尾移动, 这个过程就像冒泡一样, 直到遍历完整个数组, 完成排序
然而, 冒泡排序并不是在遍历一遍找出最大值之后, 再将最大值放到数组尾(这是选择排序)
冒泡排序, 是在一趟排序种, 如果 当前位置数值 比 +1位置数值 大, 就将数据交换位置. 如果不大, 就不做交换. 这样, 一趟遍历完成的同时, 就可以将数组中的最大值放到数组的结尾. 就像这样
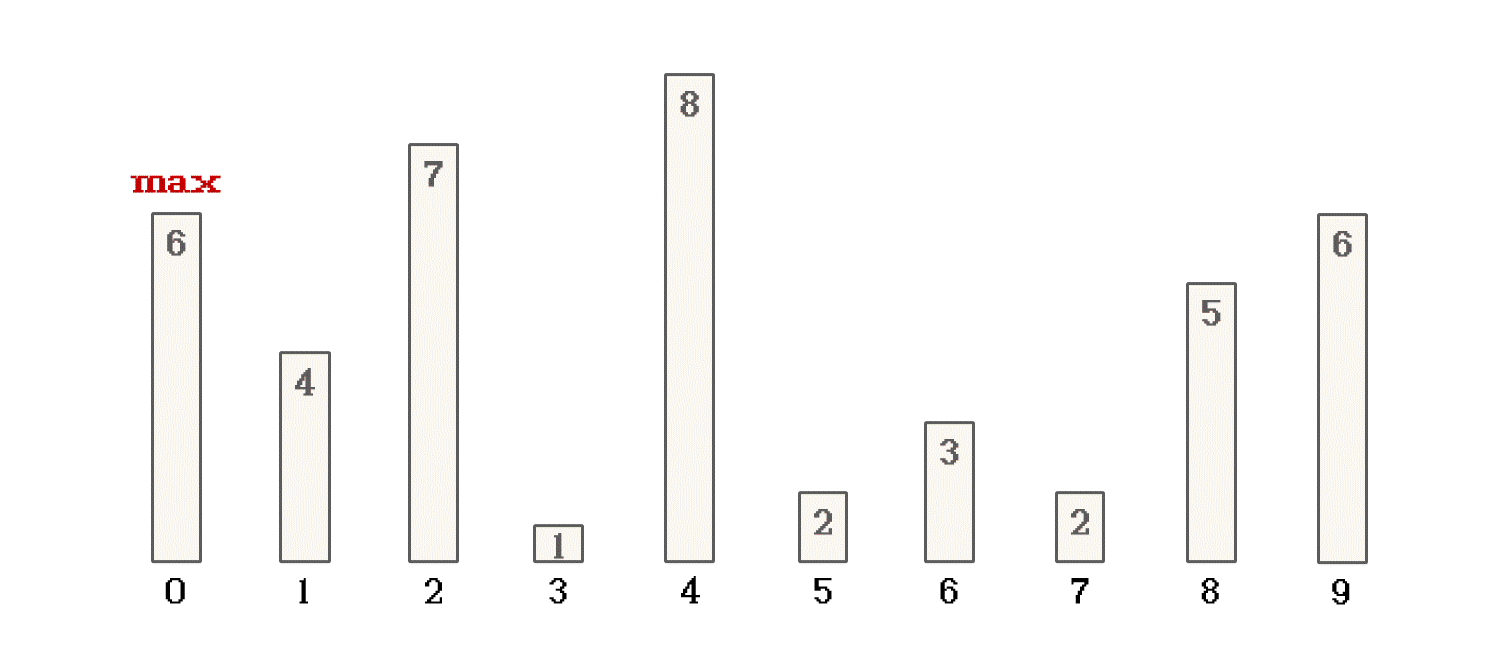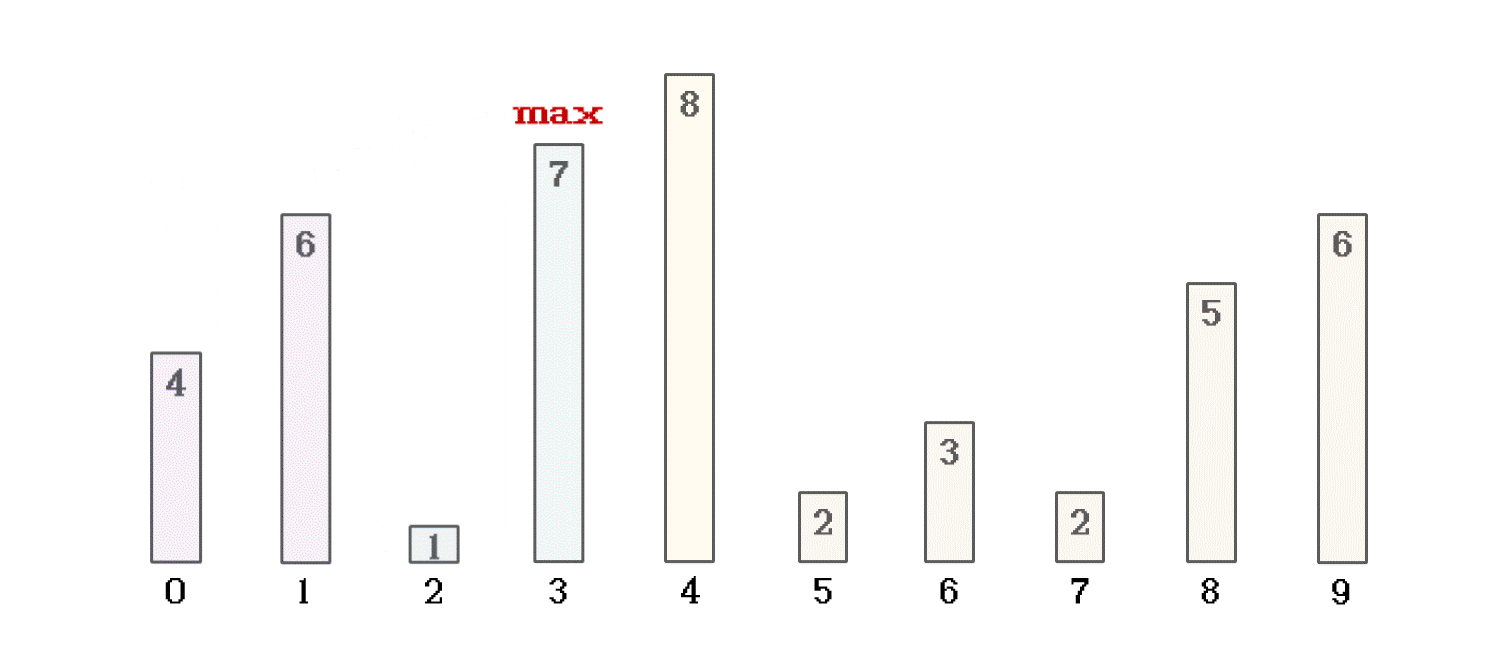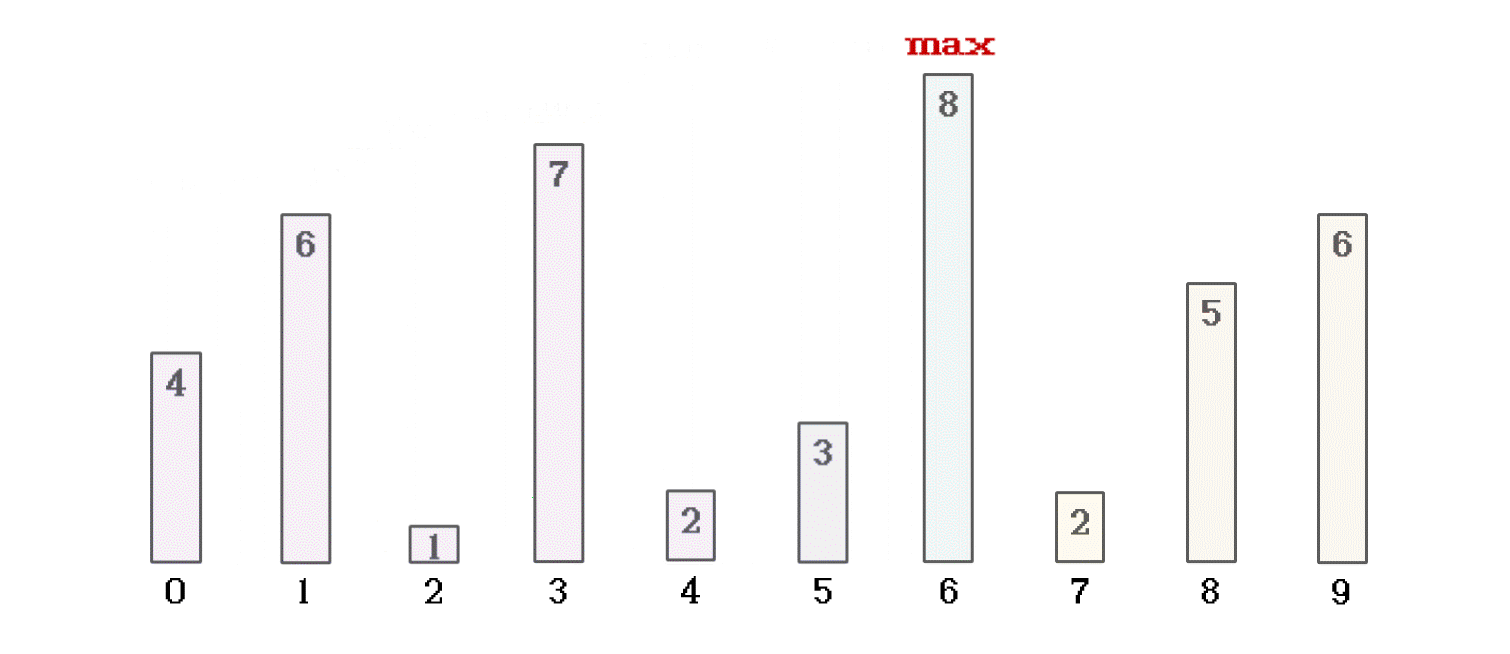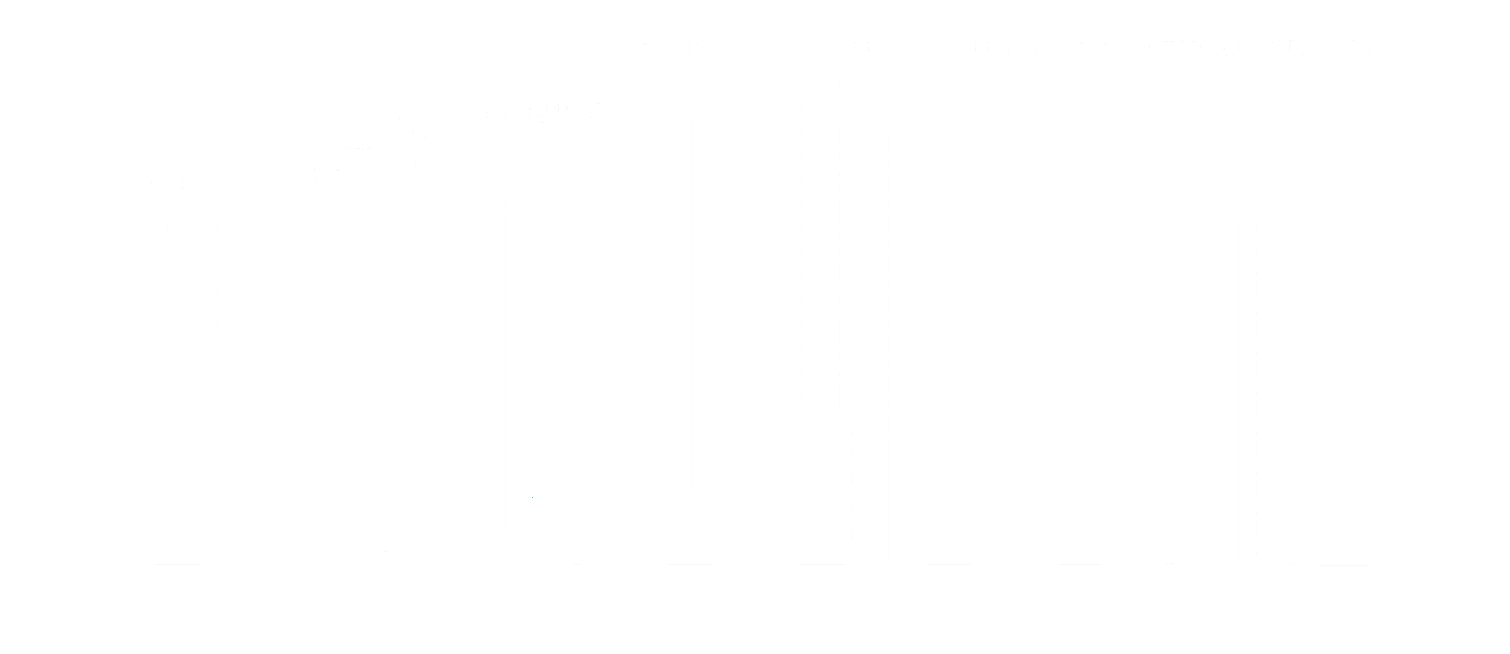
当前者大于后者时, 进行数据交换, 反之, 不做处理, 进入本趟冒泡的下一次循环
代码分析
冒泡排序实现起来, 比插入排序还要简单一些
void bubbleSort(std::vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
for (int j = 0; j < nums.size() - i - 1; j++) {
if (nums[j] > nums[j+1]) {
std::swap(nums[j], nums[j+1]);
}
}
}
}使用这段代码进行测试:
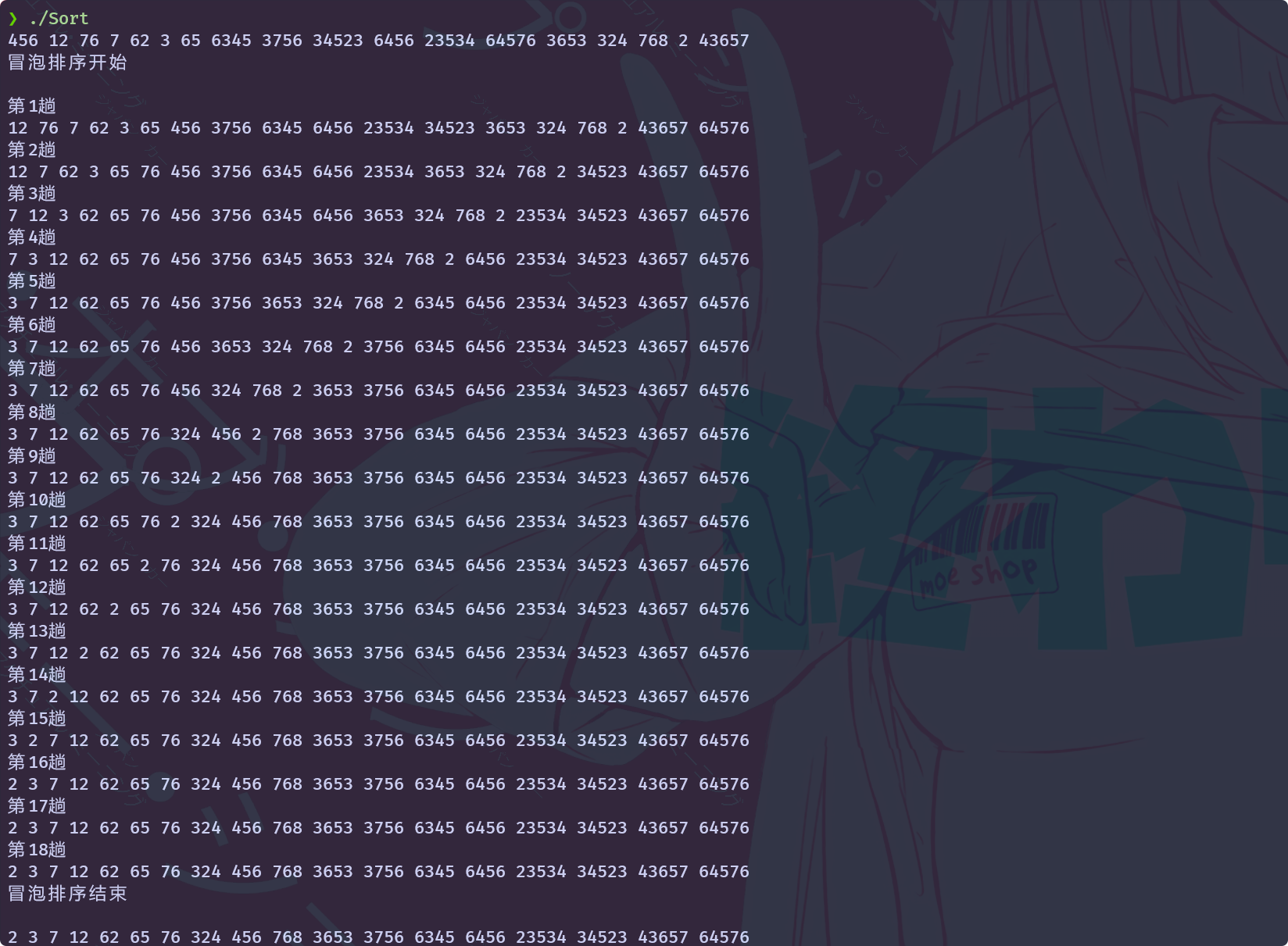
结果符合冒泡的特点
外部
for循环, 循环条件为i < nums.size(), 保证可以遍历完整个数组内部
for循环, 循环条件为j < nums.size() - i - 1减1是为了防止nums[j+1]访问越界减i则是因为每一趟冒泡, 都会有一个最大的数据置于数组尾, 那么i趟就是i个, 也就是说 数组最后i个是不用再冒泡的, 因为最后i个数据已经有序了, 即使再遍历也不会发生数据交换, 也就表示是无效遍历也就是说, 在冒泡排序中, 已经确认有序的部分不用再进行冒泡, 因为是无效冒泡, 不会发生数据交换
那么是不是可以反过来说, 在冒泡排序中, 如果某一趟冒泡没有发生数据交换, 说明整个数组有序
这个推论是成立的, 因为只有数组有序, 冒泡才不会发生数据交换
那么, 根据这个特点, 我们可以将冒泡排序的代码实现进行优化:
void bubbleSort(std::vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
int isExchange = 0; // 用于记录本趟冒泡是否发生数据交换
for (int j = 0; j < nums.size() - i - 1; j++) {
if (nums[j] > nums[j+1]) {
std::swap(nums[j], nums[j+1]);
isExchange = 1; // 发生数据交换, 置1
}
}
// 一趟冒泡结束
if (!isExchange)
break; // 如果一趟冒泡结束了, 还没有发生数据交换
// 说明整个数组已经有序了, 可以退出外部循环
}
}如果使用这段代码在进行排序, 输出的结果会有什么不同吗?

对比使用没有优化过的代码输出的结果, 少了一趟遍历
再对比第16趟和第17趟, 可以发现第17趟没有发生数据交换, 所以冒泡直接就结束了
虽然只比无优化的版本节省了一趟的消耗, 但也算是有提升
时间复杂度
冒泡排序的时间复杂度非常好计算, 两个
for循环, 最坏的情况就是 内层循环每次都要遍历完整个有效部分此时时间复杂度很明显是 O(N^2)
稳定性
在判断冒泡排序的稳定性之前, 先理解一下什么是排序的稳定性
通俗点来讲, 在数据排序前后 相等数据的相对位置没有发生变化, 我们就说此排序算法稳定
那么, 冒泡排序是否稳定呢?
冒泡排序, 只有在 前一个数 > 后一个数时, 才会发生数据交换
如果两个数相等, 不会发生数据交换
所以, 使用冒泡排序进行排序之后, 相等元素的相对位置不会发生改变
即, 冒泡排序是稳定的
选择排序
逻辑分析
选择排序的逻辑, 应该是八大排序中最简单的
最基础的选择排序, 就是 遍历N遍数组的有效范围, 每次从中找出最大值, 然后将最大值与有效范围的末尾元素进行数据交换, 最终完成排序
直到思路, 基本可以直接进行实现
代码实现
void selectSort(std::vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
int maxi = 0;
int left = nums.size() - i; // left 是每趟需要放最大值的位置
for (int j = 0; j <= left; j++) {
if (nums[j] > nums[maxi]) {
maxi = j; // 记录最大值的坐标
}
}
std::swap(nums[maxi], nums[left]);
}
}使用这段代码进行测试:
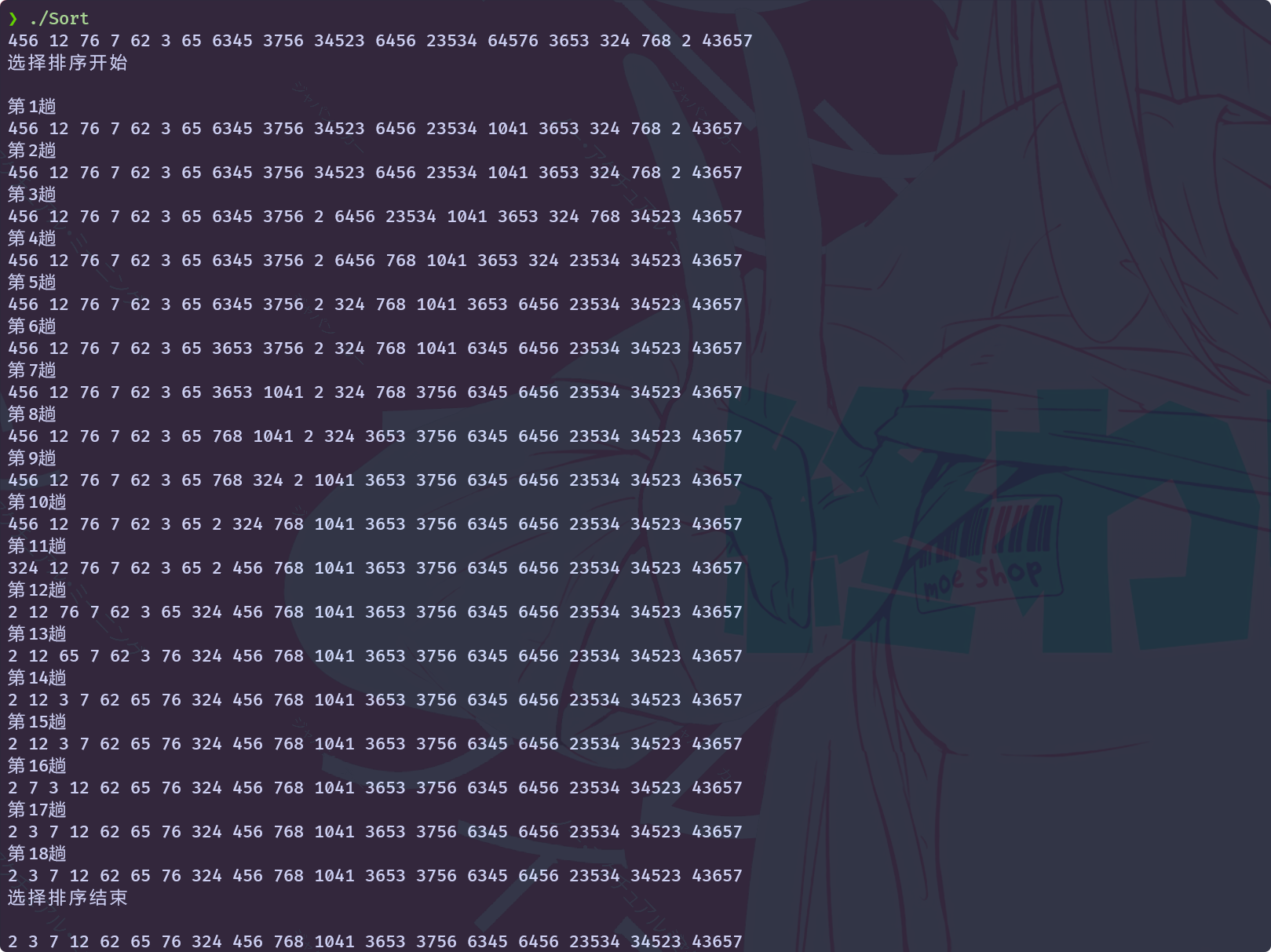
从结果看可以完成排序的, 并且每次选择一个最大值放在后面
不过, 选择排序还有优化的空间
既然每次都要在数组的有效范围内完整的遍历一遍, 那么 是不是可以 在一趟遍历中 把有效范围内的最大值和最小值一起找出来 呢?
选择排序的优化, 就是在一次遍历中找到两个极值, 然后将两个极值分别放到有效范围的双端
这样至少可以省出一半的遍历时间
实现找两个极值的方法, 有效数组的双端都会缩小, 所以不能在使用
for循环void selectSort(std::vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
// 循环停止的条件就是两指针相遇
while(left < right) {
int mini = left;
int maxi = left;
for (int i = left; i <= right; i++) {
if (nums[i] > nums[maxi])
maxi = i; // 记录最大值的位置
if (nums[i] < nums[mini])
mini = i; // 记录最小值的位置
}
// 找完极值, 就可以交换数据
std::swap(nums[maxi], nums[right]);
// 将最大值放入有效范围的末尾之后
// 不能再直接放最小值
// 因为 mini 原本可能就在有效范围的末尾, 即right
// 如果是这样, 原来的nums[mini]就被交换走了
// 此时, nums[mini]其实就是刚放入的 nums[maxi]
// 所以, 要先判断一下 mini 是否 就是right
if (mini == right) {
mini = maxi;
}
std::swap(nums[mini], nums[left]);
// 缩小有效范围
left++;
right--;
}
}使用优化过的代码进行排序, 会输出什么养的结果呢:
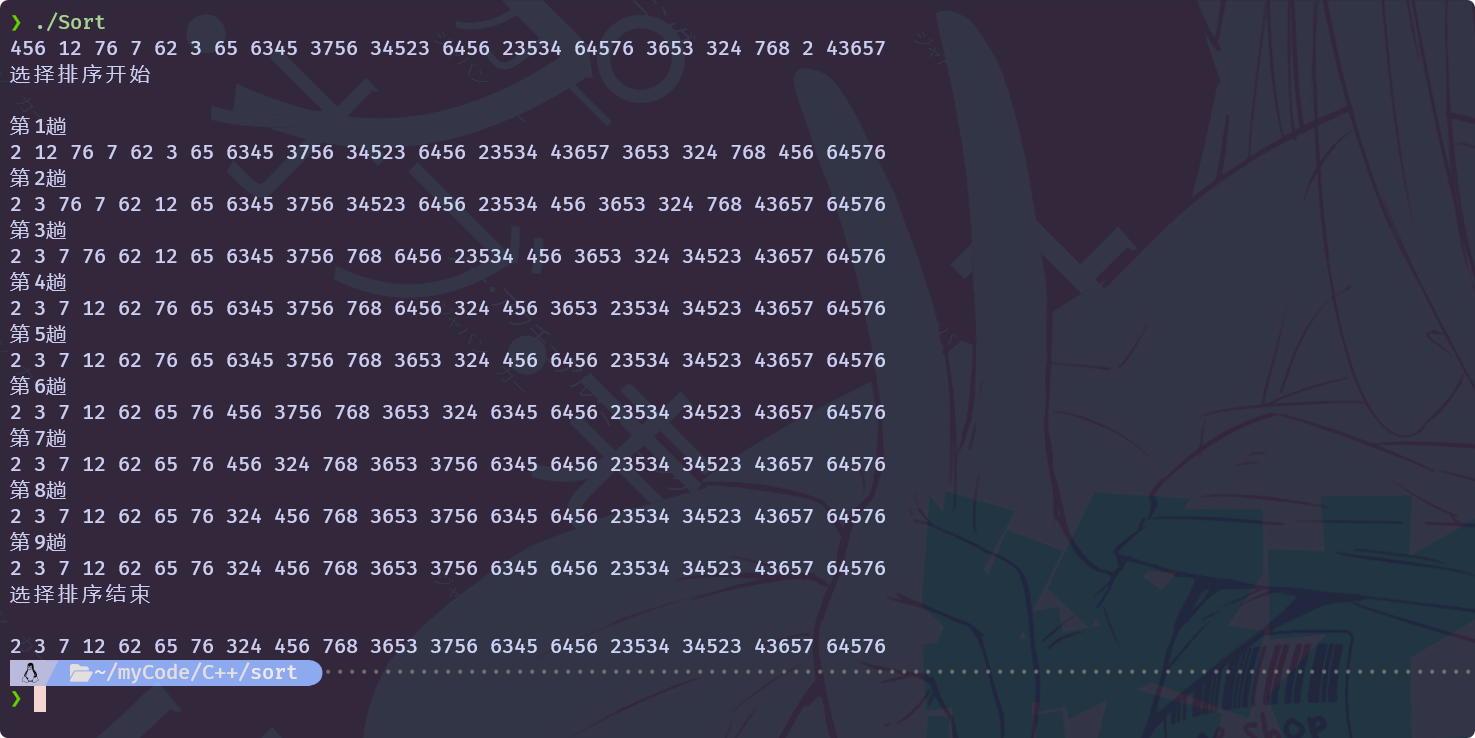
优化过的选择排序, 一共执行了9趟, 而没有优化过的选择排序则一共执行了18趟
时间复杂度
没有优化过的选择排序, 内外一共两层
for循环, 内层循环总是将有效范围的数据完整的遍历一遍, 所以时间复杂度为O(N^2)而优化过的选择排序呢?
其实还是O(N^2), 即使相比没有优化过的选择排序 循环次数减半了, 但是
1/2 * N^2分母依旧是N^2, 也就是说结果不影响大局所以, 选择排序的时间复杂度是O(N^2)
稳定性
按照选择排序的逻辑, 每次遍历选择一个极值然后放入合适的位置
如果数组中存在相同的元素, 是有可能改变相同元素之间的相对位置的
如果存在一个数组:
9 2 3 7 3 4 8 0, 那么使用选择排序, 就可能出现这种情况第1趟:
0 2 3(1) 7 3(2) 4 8 9第2趟:
0 2 3(1) 7 3(2) 4 8 9第3趟:
0 2 3(1) 4 3(2) 7 8 9第4趟:
0 2 3(1) 3(2) 4 7 8 9第5趟:
0 2 3(2) 3(1) 4 7 8 9因为,
3(1)在3(2)前面, 所以再遍历时会先遇到3(1)然后会将
3(1)放在合适的位置, 本数组中, 会将3(1)和3(2)交换位置此时, 就导致
3(1)和3(2)的相对位置发生改变所以, 选择排序会改变相同元素的相对位置
所以, 选择排序是不稳定的
插入排序
逻辑分析
插入排序, 其实从此方法的命名上, 就可以看出排序的逻辑
插入排序, 在逻辑上 将数组分为两部分:
-
[0, end], 已排序的部分, 即 已经处理过的部分这一部分, 是在排序的过程中, 一步步建立起来的
-
[end+1, size], 未排序的部分, 即 未处理的部分这一部分, 在排序过程中, 会逐步缩小
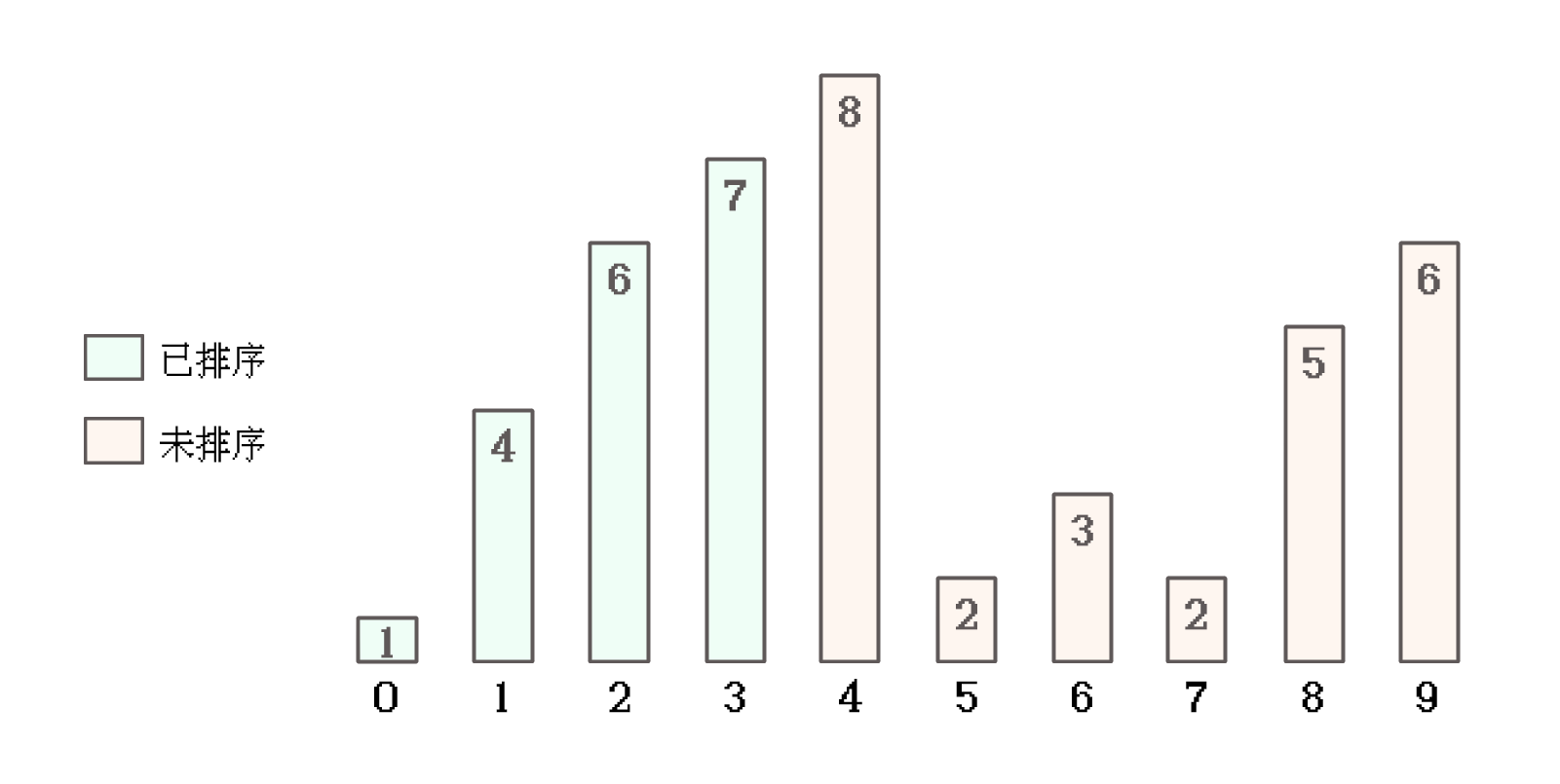
而插入排序的实现思路, 就是 拿还未排序的数据, 插入到已经排序过的部分的合适的位置, 保证前半部分依旧有序
直到逐步完成整个数组的排序
将数组
[0, end]范围 看作已经完成排序的部分, 那么[end+1, size]范围, 就是还未进行排序的部分一个还未进行排序的数组的
[0, 0]范围, 就可以看作已经完成排序的部分, 也就是数组的首元素在此基础上, 就可以拿
[1]位置数据与[0]位置数据进行对比, 查找合适的位置按照这样的思路, 那么一趟排序的过程就可以分析出来:
- 每趟排序, 拿
[end+1]位置数据,[0, end]位置数据逐一进行对比 - 比
[end+1]大的数据, 需要向后移一位给[end+1]数据腾位置 - 直到遇到
<=[end+1]的数据, 假设此位置为[now], 就将[end+1]位置数据放在[now+1]位置上
每趟排序增加一个已经排序的数据, 首趟进行时, 已排序部分的结尾位置是
[0], 第二趟进行时, 已排序部分的结尾位置是[1]也就是说, 如果存在数组
nums, 且采用for (int i = 0; i < nums.size(); i++)循环进行遍历数组时, [end]与i是同步的每趟循环 的目的是排序, 而过程 实际上就是给
nums[end+1], 在[0, end]范围内找一个合适的位置放nums[end+1], 同时保持[0, end+1]依旧有序从
[end]位置向前遍历对比时, 遇到的第一个<=nums[end+1]的数据nums[now]的后一位, 实际就是合适的位置, 也就是说[0, now]的位置上的数据是不用移动的而
>nums[end+1]的数据, 就需要向后移动一位了, 因为nums[end+1]是比它们小的 需要放在他们前面, 如果不向后移动, 就发生数组中的数据被覆盖的情况, 导致数据丢失这就是 插入排序实现的具体思路
下面是动图演示:
代码实现
先按照分析的思路, 实现一遍代码
void insertSort(std::vector<int>& nums) {
for (int i = 0; i < nums.size() - 1; i++) {
int end = i; // end 与 i同步
int cur = nums[end+1]; // 记录nums[end+1], 因为前面的数据可能要往后移动, 会覆盖掉nums[end+1], 所以需要使用变量存储nums[end+1]
int now = end; // 从 end位置开始, 向前遍历对比数据大小
// 当遍历到整个数组头结束
while (now >= 0) {
if (nums[now] > cur) { // 对比数据比cur大, 数据向后移动一位
nums[now+1] = nums[now];
now--;
}
else {
break; // 对比数据<=cur, 就表示找到了合适的位置
}
}
// nums[now] <= cur, 就表示now+1位置为合适的位置
nums[now+1] = cur;
// 一趟排序结束
}
}for循环的循环条件是i < nums.size() - 1, 也就是说最后一次循环时, i和end(与i同步)是数组倒数第二个位置那么, 将
nums[end+1]插入到有序部分中, 实际就是将数组中最后一位数据进行排序, 也就是最后一趟排序下面可以使用这段代码进行排序:

再查看我们实现的代码
你会发现, 定义的
end没有被修改过, 而now实际上每趟循环开始时, 都赋予的end的值所以, 可以将省略
now, 直接用end进行对比遍历改良后的代码:
void insertSort(std::vector<int>& nums) {
for (int i = 0; i < nums.size() - 1; i++) {
int end = i; // end 与 i同步
int cur = nums[end+1]; // 记录nums[end+1], 因为前面的数据可能要往后移动, 会覆盖掉nums[end+1], 所以需要使用变量存储nums[end+1]
// 当遍历到整个数组头结束
while (end >= 0) {
if (nums[end] > cur) { // 对比数据比cur大, 数据向后移动一位
nums[end+1] = nums[end];
now--;
}
else {
break; // 对比数据<=cur, 就表示找到了合适的位置
}
}
// nums[end] <= cur, 就表示end+1位置为合适的位置
nums[end+1] = cur;
// 一趟排序结束
}
}时间复杂度
插入排序的时间复杂度是多少呢?
首先, 外层的
for循环是必须的, 所以有至少是O(N)了那么, 内层呢?
内层最好的情况是:
nums[end]恒比nums[end+1]小, 即 原数组有序, 此时内层循环只需要执行一次, 那么整体的时间复杂度为O(N)内层最坏的情况是: 每次都要从end遍历到0, 也就表示 原数组其实就是有序的, 不过是反向有序, 即 目标排序的逆序
那么, 就是
N*N所以, 插入排序的时间复杂度实际上是O(N^2)
稳定性
我们上面分析了插入排序的逻辑, 当待插入数据首次遇到
<=它的数据时, 并没有将待插入数据存储在相应的位置上, 也没有发生数据交换而是将待插入数据放在了后一位
所以, 插入排序前后, 相等数据的位置是没有发生改变的
所以, 插入排序是稳定的
希尔排序
希尔排序, 实际是对插入排序排序的优化
逻辑分析
插入排序, 是将数组看作两部分: 已排序和未排序部分, 每次拿未排序部分的首元素 插入到 已排序部分的合适位置, 进而扩大已排序部分, 直到已排序部分扩大为整个数组, 最终完成排序
而, 希尔排序优化了插入排序
不过, 希尔排序会按照固定的间隔对数组进行分组, 然后对分组使用插入排序
如果存在一个数组:
9 2 3 7 3 4 8 0 5 6 2 1, 一共12个元素希尔排序会按照固定的间隔, 对数组进行分组, 比如以4为间隔:
-
9 3 5下标为0 4 8, 做插入排序 3 5 9
-
2 4 6下标为1 5 9, 做插入排序 2 4 6
-
3 8 2下标为2 6 10, 做插入排序 2 3 8
-
7 0 1下标为3 7 11, 做插入排序 0 1 7
分组排完序, 数组为
3 2 2 0 5 4 3 1 9 6 8 7然后呢?
然后希尔排序缩小间隔, 继续插入排序
这一次, 以2为间隔:
-
3 2 5 3 9 8下标为0 2 4 6 8 10, 做插入排序 2 3 3 5 8 9
-
2 0 4 1 6 7下标为1 3 5 7 9 11, 做插入排序 0 1 2 4 6 7
分组排序完成, 数组为
2 0 3 1 3 2 5 4 8 6 9 7希尔排序会持续缩小分组间隔, 并针对分组进行插入排序
最终, 间隔为1 直接插入排序:
0 1 2 2 3 3 4 5 6 7 8 9这样做有什么意义? 最终不还是要对整个数组进行插入排序吗?
上面分析过插入排序的时间复杂度, 在数组有序的情况下插入排序的时间复杂度是O(N)
也就是说, 数组越接近有序, 插入排序的所需时间就越短
希尔排序最终会对整个数组进行直接插入排序
而之前 对数组内容分组进行插入排序是在干什么?
在最后一次插入排序之前, 希尔排序其实在进行 预排序 , 预排序的目的, 是将整个数组尽量的趋近于有序
因为数组越接近有序, 插入排序所需的时间就越短, 所以, 预排序, 采用对数组一定的间隔进行分组插入排序的方式, 试图将数组中大的数据尽快地放在数组的后面, 小的数据尽快地放在数组的前面
上面只用文字对希尔排序的过程进行分析, 并没有那么明显, 如果以动图的形式展现出来, 就可以看出来 预排序的作用:
从排序结果来看, 第一次分组插入排序十分有效的将数组中较大的数据放在的末尾了
之后, 缩小分组间隔 进行插入排序, 可以更加细化的将数组内容趋于有序
在希尔排序中:
- 分组间隔越大, 预排序可以将较大数据和较小数据可以更快的放在数组尾和数组头
- 分组间隔越小, 预排序可以将整个数组更加趋近于有序
多次预排序之后, 最后一次直接插入排序的过程, 以动图来演示:

从演示中可以看到, 最后一次直接插入排序, 每次从
[end+1]向前对比的的次数不会超过第一次分组的间隔, 很多次甚至只需要对比一次, 不用再向前继续遍历对比这样的结果可以看出, 经过预排序之后, 确实可以为最后一次直接插入排序节省许多时间
但是, 多次的预排序+最后一次的直接插入排序, 希尔排序的时间复杂度是多少呢?
实际上, 希尔排序的时间复杂度与分组时所取的间隔(Gap)有关, 而Gap的取值是不确定的
但是, 无论Gap如何取值, 取值的方法都是前人经过大量的实验得出来的,
Gap /=2 或 Gap /= 3 或 Gap = Gap / 3 + 1等等, 但要保证最后的Gap为1而Knuth提出的
Gap = Gap / 3 + 1的方法, 在其大量的实验和统计下得出: 当数组数据很多时, 数据的平均比较次数和移动次数, 大约在N^1.25~1.6*N^1.25而下面的代码实现, 就采用
Gap = Gap / 3 + 1的方法, 所以时间复杂度 可以暂时按照O(N^1.25)~O(1.6 * N^1.25)来计算代码实现
void shellSort(std::vector<int>& nums) {
int gap = nums.size();
while (gap > 1) { // gap > 1 就继续预排序
gap = gap / 3 + 1; // 预排序 gap的取值方法
for (int i = 0; i < gap; i++) { // 外层循环次数 其实就是分出来的的组数
for (int j = i; j < nums.size() - gap; j += gap) {
int end = j; // 对以gap为间隔分组的数据, 进行插入排序
int cur = nums[end + gap];
while (end >= 0) {
if (cur < nums[end]) {
nums[end + gap] = nums[end];
end -= gap;
}
else {
break;
}
}
nums[end + gap] = cur;
}
}
}
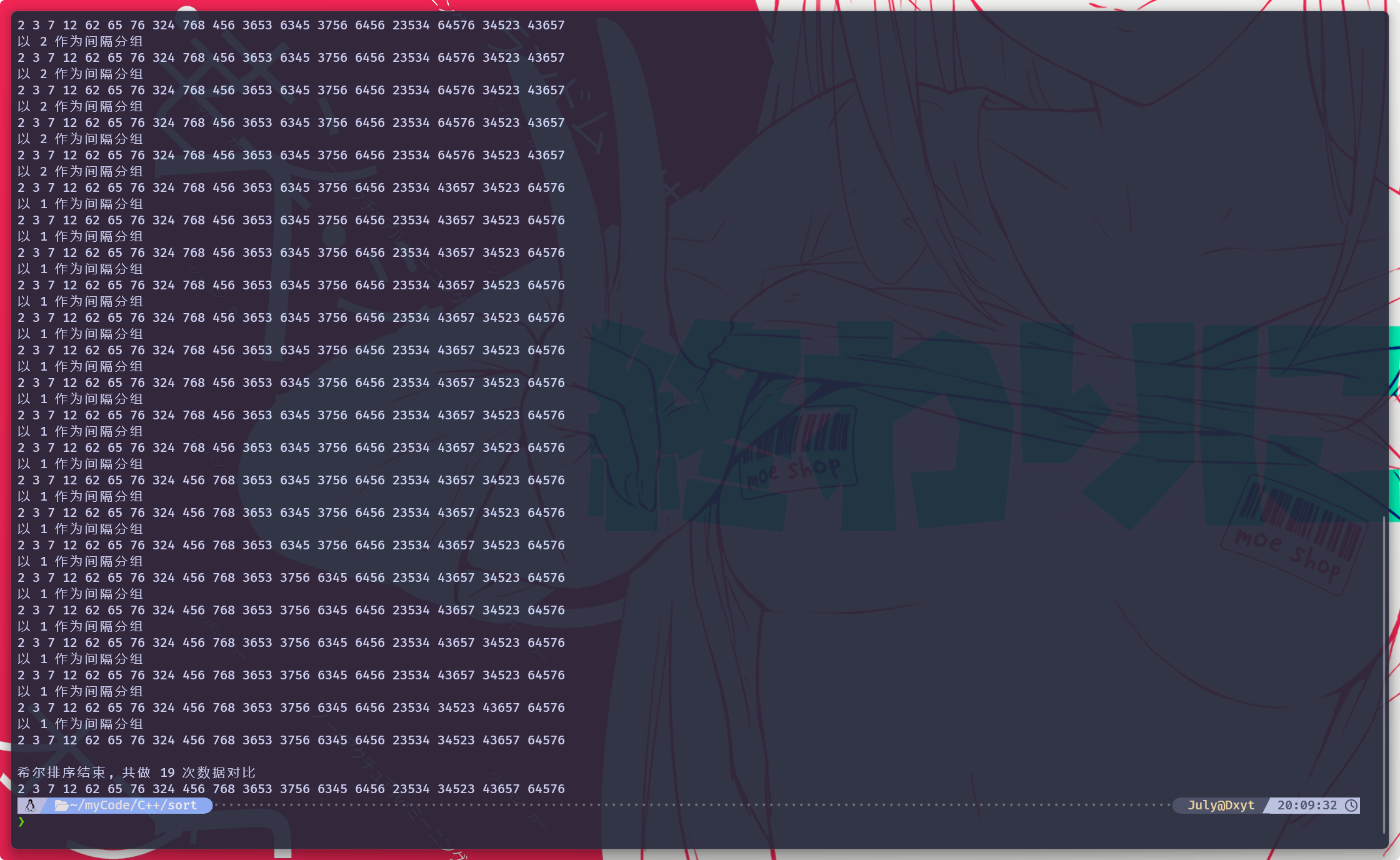
}使用这段代码进行排序:
可以正常的实现排序
但是, 会发现 希尔排序好像会经历 非常多次的循环和遍历, 好像并没有起到优化插入排序的作用
只从打印现象来看是这样的
但是, 如果 在
while循环内部记录数据的对比次数, 然后再分别测试直接插入排序和希尔排序: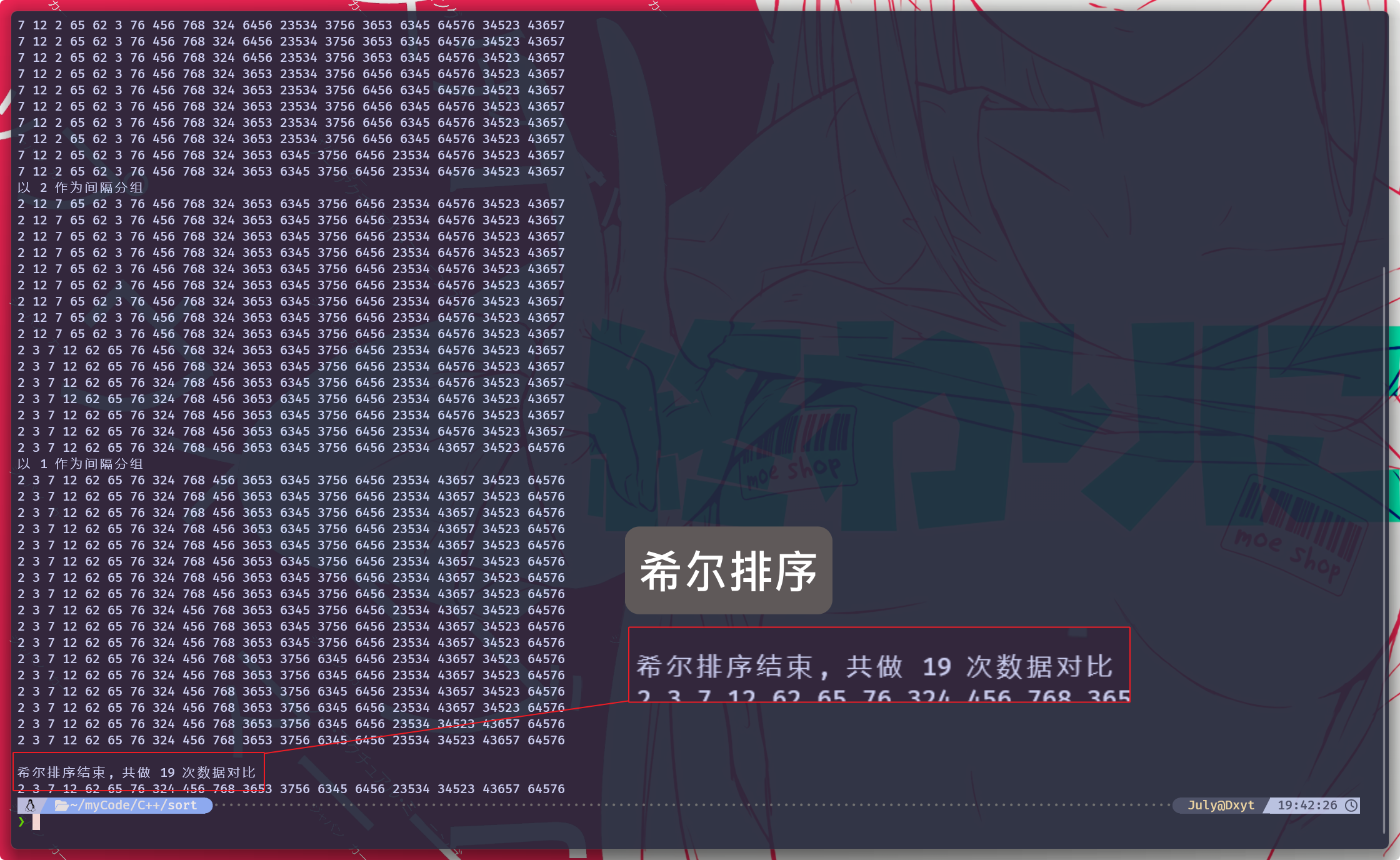
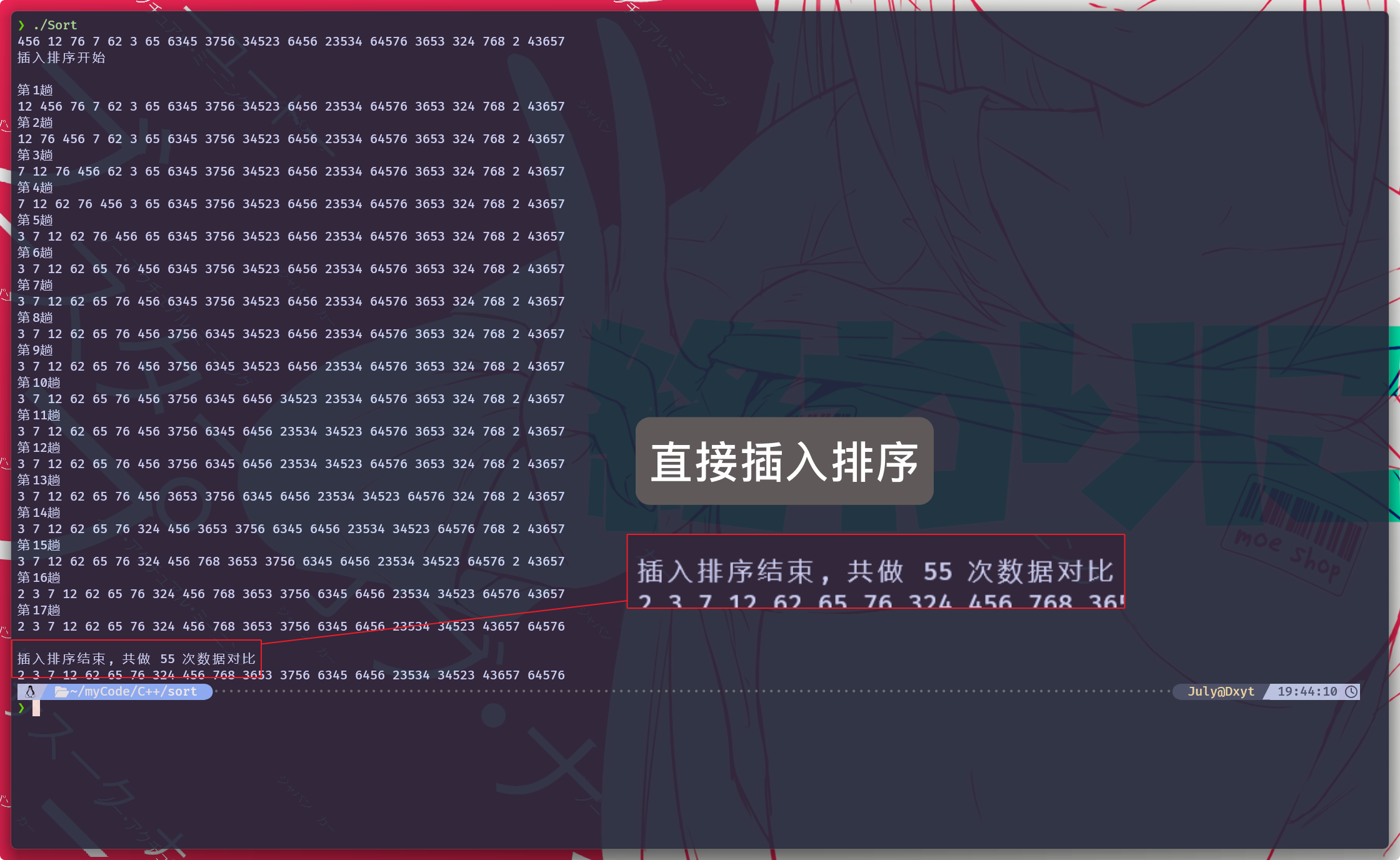
经过实际的对比可以看到, 希尔排序和直接插入排序 时间复杂度差值还是比较大的
上面的希尔排序实现代码中, 使用了三层循环:
- 最外层的
while循环, 用于对gap取值 - 第二层的
for循环, 则是用于进行gap次的分组 - 最里层的
for循环, 则是为了对每个分组的数据进行插入排序
这是最基础的, 也是最容易理解写法
还有一种写法, 可以将三层循环 优化成 两层循环嵌套, 不过实际上的时间复杂度是不会发生变化的
上面的写法, 可以理解为 先完整分组, 然后再插入排序
而实际上, 因为不用额外存储分组数据, 所以 可以不用完整的分组
void shellSort(std::vector<int>& nums) {
int gap = nums.size();
while (gap > 1) {
gap = gap / 3 + 1;
for (int i = 0; i < nums.size() - gap; i++) {
int end = i;
int cur = nums[end + gap];
while (end >= 0) {
if (cur < nums[end]) {
nums[end + gap] = nums[end];
end -= gap;
}
else {
break;
}
}
nums[end + gap] = cur;
}
}
}直接按顺序遍历数组的元素, 再遍历的过程中, 再针对遍历到的元素找其分组的元素进行插入排序
什么意思呢?
就是不再完整地一组一组的进行插入排序, 而是遍历数组元素, 遍历到某个元素, 再对此元素进行插入排序
比如:
-
i = 0时, 只对nums[0+gap], 进行插入排序接下来, i 不 += gap, 而是++
-
i = 1, 就对nums[1+gap], 进行插入排序 -
i = 2, 就对nums[2+gap], 进行插入排序 -
以此类推,
i会从0 ~ nums.size()-gap, 在这个过程中 会完整的对每个分组的数据, 在其分组中进行插入排序
不会影响排序时, 数据的对比次数, 更不会影响时间复杂度
时间复杂度
希尔排序的时间复杂度没有办法很好的计算, 不过可以看作接近
O(N*log N)稳定性
因为, 希尔排序会对数据进行分组进行插入排序, 相等的数据也会被分到不同的组, 所以 想等数据的相对位置是会发生改变的
所以, 希尔排序是不稳定的
版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
作者: 哈米d1ch 发表日期:2024 年 8 月 1 日