Leetcode 2024 年 7 月 29 日

[Leetcode] 力扣热题100道--双指针3: 15. 三数之和(中等)

给你一个整数数组 nums, 判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k, 同时还满足 nums[i] + nums[j] + nums[k] == 0. 请你返回所有和为 0 且不重复的三元组

Leetcode 算法题约2186字 -- 阅读时间≈10分钟

在做三数之和这个题之前, 最好先理解一个前置题: 167. 两数之和 II - 输入有序数组

167. 两数之和

题意分析

根据题目描述和示例分析, 本题的意思是:

给定一个有序数组, 给定一个target
数组中存在且只存在两个数的和为target, 即存在唯一解
请找到这两个数在数组中的坐标(数组坐标从1开始), 并将两坐标以vector<int>形式返回
不能额外开辟空间, 且不可以重复使用相同的元素(可能是说两个坐标不能相同? 因为两个数相同可以通过)

思路分析

这种题最简单的思路, 还是暴力遍历. 但是这样一般都无法通过

而, 在有序数组中查找数据, 处理暴力遍历, 第一个可能想到的应该是 二分查找

本题可以使用 二分查找 的方式解决:

遍历数组
遍历数组的过程中, 计算target - nums[i]
并在当前位置之后的数组中, 二分查找计算结果
直到找到

如果是在有序数组中查找一个指定的数, 那么时间复杂度为O(log N)

而本题中, 在遍历数组的过程中再使用二分查找, 时间复杂度就是 O(N*log N)

除了二分查找之外, 还有另一种解法:

双指针解法

数组有序且一定存在唯一解, 所以可以定义两个指针, 分别指向数组的首尾元素

然后对比两指针指向数据之和与 target

当 target大, 就表示left指向元素小了, 就需要left++
当 target小, 就表示right指向元素大了, 就需要right--

可以这样解决的前提是, 数组非递减有序

left的初始位置是数组首元素, 也就是数组中最小的数

right的初始位置是数组尾元素, 也就是数组中最大的数

此时, 如果nums[left] + nums[right] < target, 就说明nums[left]拖后腿了, 就需要增大nums[left], 即left++

反之, 如果nums[left] + nums[right] > target, 就说明nums[right]大了, 就需要减小nums[right], 即 right--

这种解法, 只需要最多只需要遍历一遍数组, 就可以找到答案

代码实现

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        // 2. 二分查找 (可过) 时间复杂度为O(N*log N)
        // vector<int> ret;
        // for (int i = 0; i < numbers.size(); i++) {
        //     int sub = target - numbers[i];
        //     int left = i + 1;
        //     int right = numbers.size();
        //     int midIndex = (left + right) / 2;
        //     while (left < right) {
        //         if (numbers[midIndex] > sub) {
        //             right = midIndex;
        //         }
        //         else if(numbers[midIndex] < sub) {
        //             left = midIndex + 1;
        //         }
        //         else {
        //      	   ret.push_back(i + 1);
        //      	   ret.push_back(midIndex + 1);
        //      	   break;
        //         }
        //      
        //         midIndex = (left + right) / 2;
        //     }
        //    if (!ret.empty())		// 结果数组中已存在数据, 表示已找到
        //       break;
        // }
        //
        // return ret;

        // 3. 双指针 (最多只遍历一边数组) 时间复杂度O(N)
        int left = 0;
        int right = numbers.size() - 1;

        vector<int> ret;

        while (left < right) {
            int addRst = numbers[left] + numbers[right];
            if (addRst < target)
                left++;
            else if (addRst > target)
                right--;
            else {
                ret.push_back(left + 1);
                ret.push_back(right + 1);
                break;
            }
        }

        return ret;
    }
};

理解了两数之和之后, 下面看一下三数之和

15. 三数之和

题意分析

根据题目描述和示例分析, 本体的意思是:

给定一个数组, 数组中可能存在 nums[i] + nums[j] + nums[k] == 0
三个元素为数组中不同位置的数据
三个这样的元素组成一个三元组, 数组中可能存在元素重复的三元组, 也可能不存在符合条件的三元组
请统计所有符合要求, 且元素不重复的三元组, 并返回
统计的三元组不可重复

即, 不可同时返回类似 {-1, 0, 1} {0, -1, 1} {1, 0, -1} 的三元组, 只能返回其中一个

思路分析

在做过 167. 两数之和之前, 如果没有时间的限制, 本题可以使用O(N^3)时间复杂度的暴力解法

但是, 很明显是有时间复杂的限制的, 并且O(N^3)的时间复杂度也确实太慢了

而在做过 167. 两数之和之后, 很容易可以想到相同的方法

但是, 本题与167不同的是:

本题数组乱序
本题需要找满足要求的三个元素, 组成三元组
本题可能存在元素重复的结果, 而最终结果需要去重

1, 很好解决: sort()

2, 排序之后, 如果不需要去重, 可以尝试沿用类似 167 的双指针法, 只不过本题中换成三指针

first指针指向第1个元素, second去寻找第2个元素, third寻找第3个元素

只要固定first, second和third就可以使用双指针法来确定

所以, 最外层循环可以用first遍历数组, 针对每一个first, target = -nums[first], 这样就算是固定了first, 内层循环就尝试用second和third双指针, 寻找nums[second] + nums[third] = target

这样内层循环就变成了 167. 两数之和 的思路

但是, 167 有且只有唯一解, 找到就可以直接返回, 而本题 不仅需要找到所有满足要求的三元组, 还需要对重复元素的三元组去重

这样看, 如果依旧不做优化的进行遍历, 也依旧是O(N^3)的时间复杂度, 再加上去重的要求可能更加雪上加霜

那么, 本题该如何实现?

大致思路已经有了, 先排序, 再三指针简化为两指针遍历, 再去重

那么有没有可能将2 3的处理合在一起进行?

先对数组进行排序, 那么数组就会变成非递减的数组

以一个简单的数组举例, 数组元素位置会发生变化:

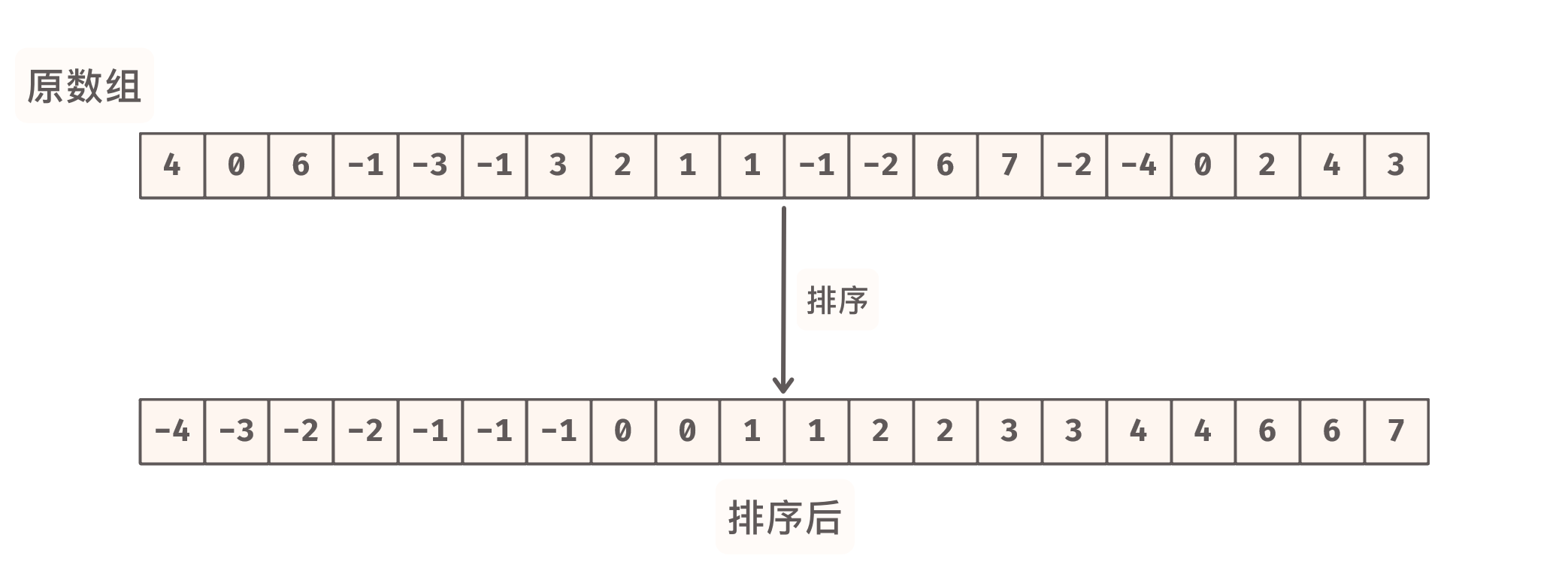
对于有序的、有重复元素的数组, 有一个很明显的现象: 存在一些相同元素的连续序列

这有利于去重, 并优化遍历数组的次数

因为 无论是固定first还是查找second, 都可以只用这些相同元素连续序列的首元素来进行处理, 其他部分可以忽略

这样不仅忽略的重复的无效元素, 也有效的减少了数组的遍历次数

所以对于本题, 可行的思路是:

先对数组进行排序, 将数组非递减有序化
使用first指针遍历数组, 但是对重复的元素只使用第一个重复元素进行查找second和third, 忽略其他相同的重复元素
固定first之后, 也就确定了nums[second]+nums[third]
可以使用与确定first相同的思路, 尝试遍历并固定second
然后再遍历确定third
一组三元素确定之后, 以vector<int>的形式存储到vector<vector<int>>中
直到first遍历完整个数组
最后返回结果数组

代码实现

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int numsSize = nums.size();

        vector<vector<int>> ret;

        // 先排序
        sort(nums.begin(), nums.end());

        for (int firstIndex = 0; firstIndex < numsSize - 2; firstIndex++) {
           	// firstIndex == 0时, 不跳过本次循环直接进入secondIndex的查找
            if (firstIndex > 0 && nums[firstIndex] == nums[firstIndex - 1])
                continue;
            
            // 当firstIndex位置的数据已经>0
            // 就说明 数组从此位置开始,  之后的所有数据都>0
            // 后面也就不存在 任意三个元素加为0的三元组
            // 所以直接跳出整个循环
            if (nums[firstIndex] > 0)
                break;
            
            // 走到这里, 就说明nums[firstIndex] 是整个数组的首元素 或 nums[firstIndex] != nums[firstIndex-1], 即nums[firstIndex]就是新相同元素序列的第一个元素
            // 就可以从firstIndex + 1位置, 开始尝试确认第二个元素
            int thirdIndex = numsSize - 1;
            int satTarget = -nums[firstIndex];
            for (int secondIndex = firstIndex + 1; secondIndex < numsSize - 1; secondIndex++) {
                // 相同的思路, 尝试确认第二个元素
                if (secondIndex > firstIndex + 1 && nums[secondIndex] == nums[secondIndex - 1])
                    continue;
                
                // 从数组尾, 遍历查找第三个元素
                while (secondIndex < thirdIndex && 
                       nums[secondIndex] + nums[thirdIndex] > satTarget)
                    thirdIndex--;
                
                if (secondIndex == thirdIndex)
                    break;
                    // 这意味着, nums[thirdIndex]最小时, 也没能找到目标 thirdIndex, 后续的遍历就不必了
             
                // 如果找到了, 就存储 记录
                if (nums[secondIndex] + nums[thirdIndex] == satTarget)
                    ret.push_back(vector<int>{nums[firstIndex], nums[secondIndex], nums[thirdIndex]});
            }
        }

        return ret;
    }
};

作者：哈米d1ch 发表日期：2024 年 7 月 29 日

[Leetcode] 力扣 热题100道--双指针3: 15. 三数之和(中等)

167. 两数之和

题意分析

思路分析

代码实现

15. 三数之和

题意分析

思路分析

代码实现

[Leetcode] 力扣热题100道--双指针3: 15. 三数之和(中等)