数据结构 2022 年 5 月 1 日

[数据结构] 结合题目-手把手带你剖析 “带环链表”

本篇内容是对单链表的一个非常重要的补充: 带环单链表。它, 是大厂面试时可能会提问的内容, 非常的重要！

数据结构算法链表约3682字 -- 阅读时间≈15分钟

引言

上一篇 【神秘海域】数据结构与算法 内容是 单链表及其接口

而本篇内容是对单链表的一个 非常重要 的补充: 带环单链表 。它, 是大厂面试时可能会提问的内容, 非常的重要！

本篇就是要结合题目来详细分析一下 单链表的带环问题

带环单链表之前 : 快慢指针

在详细分析带环单链表之前, 先分析两道题来了解一个非常重要的算法思路: 快慢指针

题1: 单链表的中间结点

原题描述是这样的:

给定一个头结点为 head 的非空单链表, 返回链表的中间结点。

如果有两个中间结点, 则返回第二个中间结点。

示例 1:

输入: [1,2,3,4,5]

输出: 此列表中的结点 3 (序列化形式: [3,4,5])

返回的结点值为 3 (测评系统对该结点序列化表述是 [3,4,5])

注意, 我们返回了一个 ListNode 类型的对象 ans , 这样:

ans.val = 3 , ans.next.val = 4 , ans.next.next.val = 5 , 以及 ans.next.next.next = NULL

示例 2:

输入: [1,2,3,4,5,6]

输出: 此列表中的结点 4 (序列化形式: [4,5,6])

由于该列表 有两个中间结点 , 值分别为 3 和 4, 我们 返回第二个结点

原题链接: Leetcode - 876. 链表的中间结点

这一题的解法, 就需要使用到 快慢指针 的思路

那么什么是 快慢指针 ？即, 使用两个 移动速度不同 的指针在 数组 或 链表 等序列结构上移动。

本题思路:

求链表的中间节点, 就可以定义两个指针 : pslow 慢指针 、 pfast 快指针

在本题中, 快指针每次 移动两个节点 , 慢指针每次 移动一个节点 , 当快指针 走过尾节点为空(链表节点为单数) 或指向尾节点(链表节点为双数) 时, 慢指针应该 正好在中间节点

此时 慢指针所指节点 即为题目所求

代码实现:

struct ListNode* middleNode(struct ListNode* head)
{
    struct ListNode* pfast = head;
    struct ListNode* pslow = head;
    while(pfast && pfast->next)
    {
        pfast = pfast->next->next;
        pslow = pslow->next;
    }

    return pslow;
}

题2: 链表中倒数最后k个结点

此题描述是这样的:

例如, 输入 {1,2,3,4,5}, 2 时, 对应的链表结构如下图所示:

其中蓝色部分为该链表的最后2个结点, 所以 返回倒数第2个结点（也即结点值为4的结点） 即可, 系统会打印后面所有的节点来比较。

示例 1:

输入: {1,2,3,4,5},2

返回值: {4,5}

说明: 返回倒数第2个节点4, 系统会打印后面所有的节点来比较。

示例 2:

输入: {2},8

返回值: {}

原题链接: Nowcoder - JZ22 链表中倒数最后k个结点

本题的思路也是使用快慢指针, 但是与上一题不同的是, 本题是先走为快指针与后走为慢指针

本题思路:

定义两个指针 : pslow 慢指针 、 pfast 快指针, 两指针均 一步一步走

快指针先走 k 步, 但同时要保证 快指针没走到空 , 如果 k 步没走完就已经走到空了, 就表示链表没那么长

然后慢指针与快指针同时开始走, 直到快指针走到空

此时 慢指针所指节点 即为题目所求

代码实现:

struct ListNode* FindKthToTail(struct ListNode* pHead, int k )
{
    struct ListNode* pfast = pHead;
    struct ListNode* pslow = pHead;
    
    while(k--)
    {
        if(pfast)
        {
            pfast = pfast->next;
        }
        else
        {// 快指针指向空, 即链表长度不到 k, 直接返回 NULL
            return NULL;
        }
    }
    while(pfast)
    {
        pfast = pfast->next;
        pslow = pslow->next;
    }

    return pslow;
}

在分析带环链表之前, 需要需要了解一下 快慢指针 , 因为 带环链表的分析 是根据 快慢指针 分析的.

带环链表分析

分析 带环链表 , 先由一道题来引入:

题: 环形链表

此题描述:

给你一个链表的头节点 head , 判断链表中是否有环。

如果链表中有某个节点, 可以通过连续跟踪 next 指针再次到达, 则链表中存在环。为了表示给定链表中的环, 评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。(注意: pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况)

如果链表中存在环 , 则返回 true 。否则, 返回 false 。

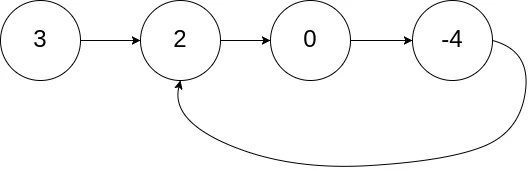
示例 1:

输入: head = [3,2,0,-4], pos = 1

返回: true

解释: 链表中有一个环, 其尾部连接到第二个节点

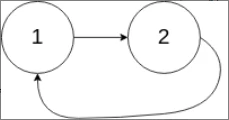
示例 2:

输入: head = [1,2], pos = 0

返回: true

解释: 链表中有一个环, 其尾部连接到第一个节点

示例 3 :

输入: head = [1], pos = -1

返回: false

解释: 链表中没有环

原题链接: Leetcode - 141. 环形链表

本题的思路也非常简单:

如果链表带环, 那么使用 快慢指针: pfast一次走两步, pslow一次走一步

两个指针就一定能相遇, 因为 两指针均入环之后, 两指针的距离是在一步步靠近的

不能相遇, 就代表 链表不带环

代码实现:

bool hasCycle(struct ListNode *head)
{
    if(head == NULL)
        return false;

    struct ListNode* pfast = head;
    struct ListNode* pslow = head;

    while(pfast && pfast->next)
    {
        pfast = pfast->next->next;
        pslow = pslow->next;

        if(pfast == pslow)
            return true;
    }

    return false;
}

OK, 带环链表的题做出来了

但是并没有结束 ~~如果只是这样怎么会有大厂提问呢？~~

带环链表的问题

在 链表带环 的基础上, 还会延伸出几个问题:

快指针一次走两步, 慢指针一次走一步, 两指针一定会相遇吗？为什么？
如果快指针一次走两步呢？三步呢？四步呢？为什么？
怎么找到带环链表的 入环节点 ？

这才是 带环链表 真正需要知道的东西~

带环链表深入分析 *

问题1

快指针一次走两步, 慢指针一次走一步, 两指针一定会相遇吗？为什么？

来详细分析一下:

画图抽象图来分析, 一个带环链表, 抽象的形式可以看作:

快慢指针 同时 从首节点开始走, 快指针走得快, 慢指针走得慢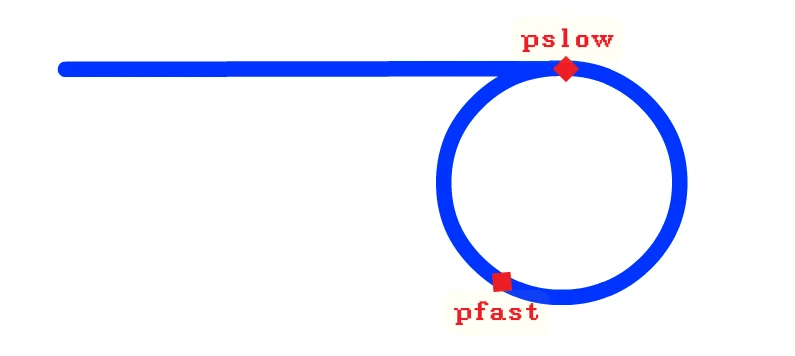

所以慢指针入环时, 快指针早就已经入环了

此时的情况可能是(设一下, 只是假设):

两个指针都入环之后, 快指针开始在环内追逐慢指针:

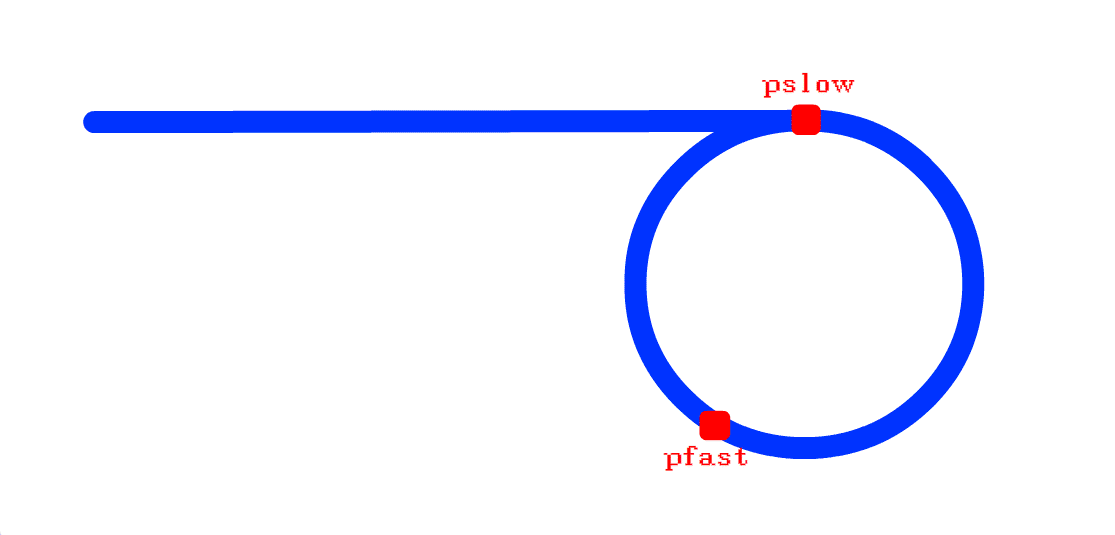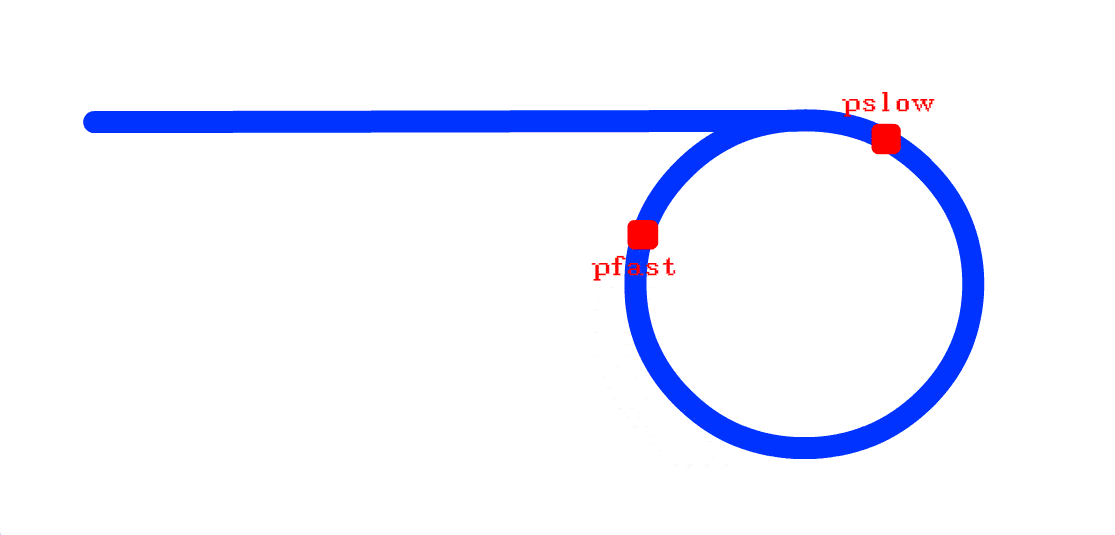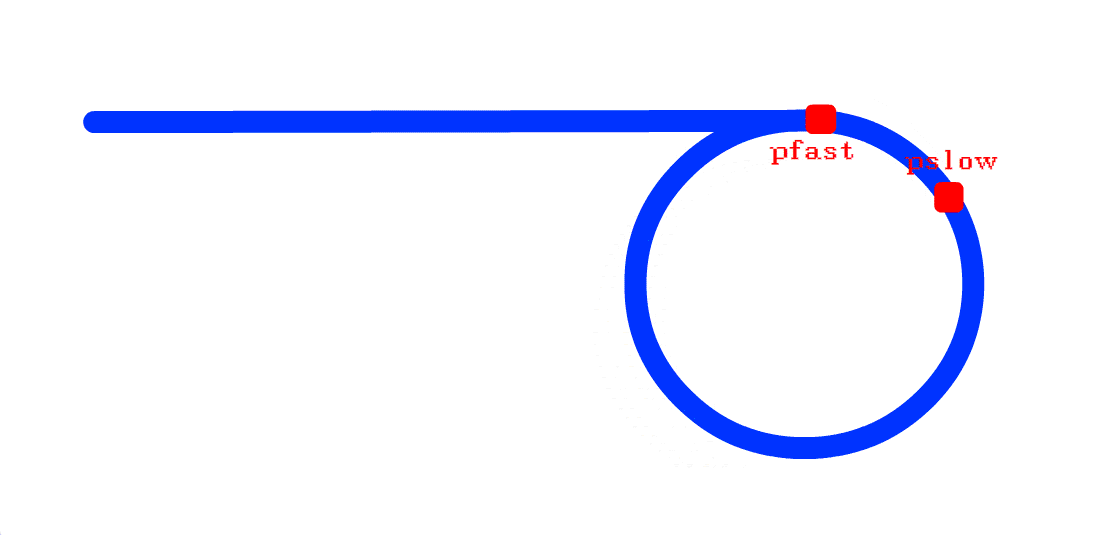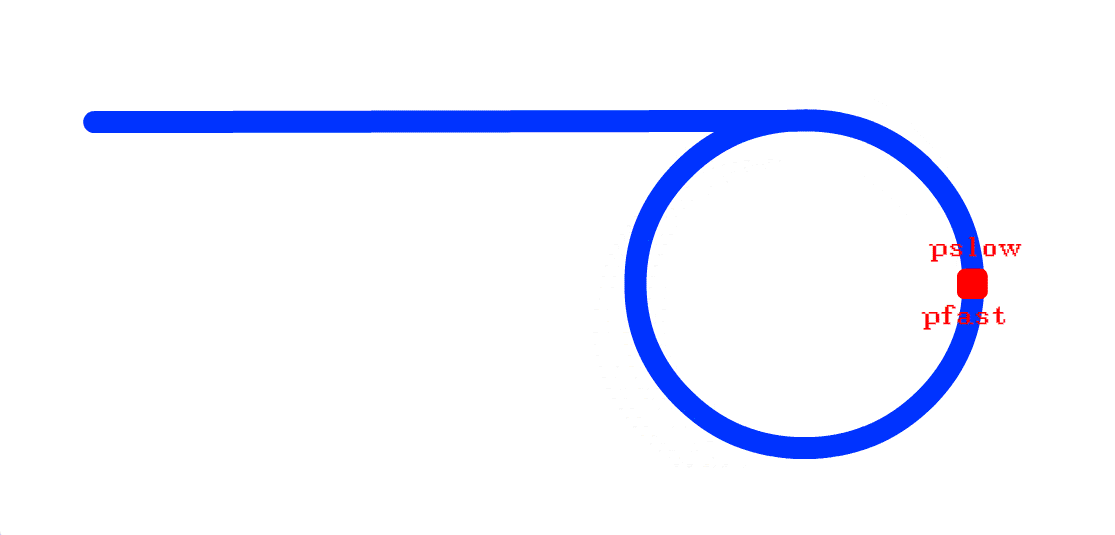
因为 当这样的两个指针都入环之后, 两个指针之间的距离变化就变为了每走一步减一

所以, 必定会相遇

问题2

如果快指针一次走三步呢？四步呢？为什么？

快指针一次走多步, 就需要看情况来分析了

快指针一次走三步:

上边我们分析了快指针一次走两步 时的相遇情况: 当两个指针都入环之后, 其之间的距离是以 每次缩小 1 变化的

那么如果 快指针一次走三步, 那么两个指针都入环之后, 其之间的距离就是以 每次缩小 2 变化的

每次缩小 2, 会造成什么情况呢？

设慢指针入环时, 快指针和慢指针之间的距离为 X, 环的长度为 C, 那么就会有两种情况: 当 X 为奇数, 当 X 为偶数

情况 1: X 为偶数

当 X(两指针之间的距离) 为偶数, 两指针距离又是 每次减2 的变化, 所以一定能相遇

情况 2: X 为奇数

此情况, 快指针超过慢指针, 但是由于快指针的移动是不连续的, 所以两指针并不会相遇

其之间的距离变成了 -1, 但是现在并不能直接判断是否能相遇, 因为不能保证后面的追击能不能相遇

又因为我们设环的长度为 C, 所以此时两指针之间的距离也是 C-1

所以, 就又分为了两种情况: 当 C-1 为奇数, 当 C-1 为偶数

当 C-1 为偶数的时候, 这时, 下次追击就可以相遇

当 C-1 为奇数的时候, 这时, 就永远不会相遇了

为什么永远不会相遇？

当 C-1 为奇数时, 也就意味着本次追击的 X(两指针之间的距离) 为奇数

X 为奇数, 就又会出现两指针之间的距离等于 -1 的情况, 距离就有变成了 C-1

所以, 当 C-1 为奇数时, 永远不会遇到

快指针一次走四步:

当快指针 一次走四步 的时候, 按照 一次走三步 的思路进行分析

X 为 3 的倍数, 可以相遇
X 不为 3 的倍数, 且 C-1 或 C-2 也不为 3 的倍数, 就永远无法相遇
C-1 和 C-2 , 需要更详细的分析

也就是说, 快指针 一次走多步 能不能与慢指针相遇是 不确定的。

实际的情况, 与 环的长度 和 入环前链表的长度 都有关系, 需要 具体情况具体分析

问题3

怎么找到带环链表的 入环节点 ？

能够找到入环节点的一个前提是: 快指针已经与慢指针相遇。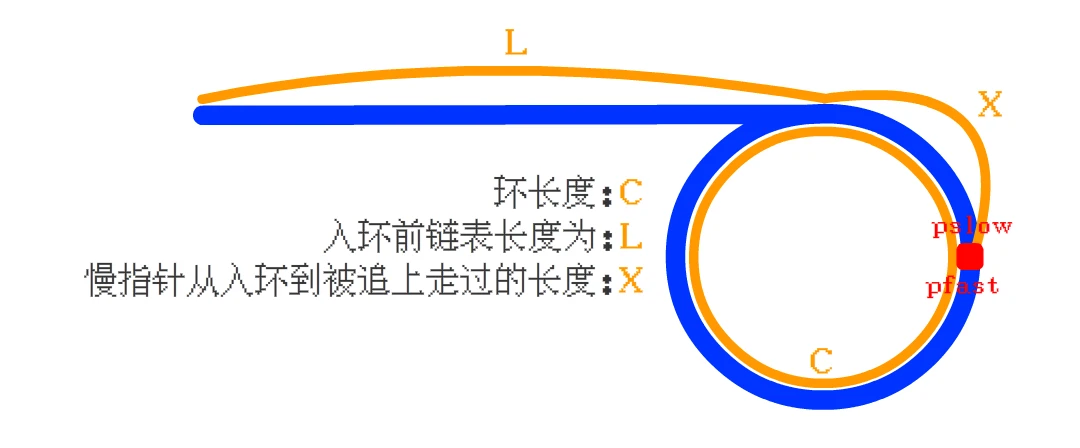

详细分析一下:

首先还是画图假设一下:

先思考一个问题: 慢指针 从入环到被追上 , 走过的长度是不是如假设的那样, 会不会已经走了一圈后才被追上的？

答案是: 不会 。

即使环再小, 只有一个节点, 慢指针那么在入环的一刻, 就已经与快指针相遇了

如果环再长, 慢指针也不可能走过一圈, 因为快指针的速度是慢指针的两倍, 慢指针如果走 超过一圈 , 那么快指针只会走 超过两圈

所以, 慢指针一定是 在一圈之内被追上的, 所以假设是成立的。

参考图来看, 慢指针 从开始 到 与快指针相遇, 走过的距离就是 : L + X

那么快指针走过的距离就是 : 2 * (L + X)

快指针走过的距离还可以怎么表示呢？

快指针走过的距离还可以这样表示: L + X + N * C (N表示走过的圈数)

因为快指针先入环, 所以在慢指针入环之前, 快指针很可能在环内已经走过几圈了

当 L 很大 C很小时, 快指针可能已经走了 N 圈了

当 L 很小 C 很大时, 快指针可能没有走超过一圈

所以, 快指针 从开始 到 与慢指针相遇 走过的距离, 就可以写成一个等式:

2 * (L + X) = L + X + N*C

化简一下就是: L + X = N * C

这个式子有什么用呢？

其实, 这个等式说明:

==如果, 有两个指针同时以一次一步的速度, 一个从 链表的首节点 开始, 另一个从 快慢指针相遇点 开始, 两个指针会在环的入口节点相遇。==

为什么呢？

L + X = N * C 可以写为 —> L = N * C - X

一个指针从链表首届点开始走, 走过 L 长度它的位置在入环节点

一个指针从快慢指针相遇点开始走, 走过 N * C 的长度, 它的位置还在快慢指针相遇点 , 但是如果走过 N * C - X 的长度, 那么它的位置就也在入环节点了, 因为 入环节点到快慢指针相遇点的距离是 X

此时, 入环节点就找到了。

题: 寻找入环节点

分析完如何寻找入环节点, 下面来尝试把这道题给做了:

题目描述:

给定一个链表的头节点 head , 返回链表开始入环的第一个节点。如果链表无环, 则返回 null。

如果链表中有某个节点, 可以通过连续跟踪 next 指针再次到达, 则链表中存在环。

为了表示给定链表中的环, 评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置**（索引从 0 开始）**。如果 pos 是 -1, 则在该链表中没有环。

注意: pos 不作为参数进行传递, 仅仅是为了标识链表的实际情况

不允许修改链表

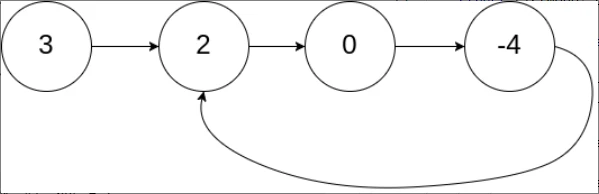
示例 1:

输入: head = [3,2,0,-4], pos = 1

输出: 返回索引为 1 的链表节点

解释: 链表中有一个环, 其尾部连接到第二个节点

示例 2:

输入: head = [1,2], pos = 0

输出: 返回索引为 0 的链表节点

解释: 链表中有一个环, 其尾部连接到第一个节点

示例 3:

输入: head = [1], pos = -1

输出: 返回 null

解释: 链表中没有环

原题链接: Leetcode - 142. 环形链表 II

代码实现:

// 大体思路与判断有环差不多
// 但是 有环时不能直接返回
struct ListNode *detectCycle(struct ListNode *head)
{
    if(head == NULL)
        return NULL;

    struct ListNode* pfast = head;
    struct ListNode* pslow = head;

    while(pfast && pfast->next)
    {
        pfast = pfast->next->next;
        pslow = pslow->next;

        if(pfast == pslow)		// 有环
        {
            struct ListNode* phead = head;
            while(phead != pslow)		//使 两个指针 分别从 首节点和相遇点 一次一步 移动, 直到相遇
            {
                phead = phead->next;
                pslow = pslow->next;
            }
            return phead;
        }
    }

    return NULL;
}

结语

本篇是对 单链表带环问题 的一个深入探索, 单链表带环问题是单链表中一个非常重要的应用和对单链表非常重要的理解。同时, 他已经进入了大厂面试可能会考的范畴, 重要的是对 单链表带环问题的深入分析 , 而不是简单的判断是否有环。

本篇文章到此结束

感谢阅读~

作者：哈米d1ch 发表日期：2022 年 5 月 1 日