[数据结构] 数据结构与算法初探: 复杂度详解分析
复杂度 引言
复杂度时间、空间, 被称为 时间复杂度、空间复杂度。
时间复杂度 主要衡量一个算法的运行快慢
空间复杂度 主要衡量一个算法运行所需要的额外空间N, 那复杂度就有可能是: N 、 logN 、N*logN 、N^2 等等。时间复杂度
时间复杂度 主要衡量一个算法的运行快慢。
但是, 这里的 快慢 并不是指 算法运行所需要执行的具体的时间。而是指: 算法中的基本操作的执行次数。并且, 算法的时间复杂度用一个函数表示.// 一个简单的循环
void Fun1(int n)
{
for(int i = 0; i < n; i++)
{
printf("%d ", i);
}
}for 循环执行的次数, 是根据传入的参数来具体决定的, 即循环 n 次。就可以说, 这个函数的 时间复杂度是 O(N)。void Fun2(int n)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
}Fun2 中存在三个循环体, 其中一个是嵌套的双重循环
那么, 这个函数的 时间复杂度 是多少呢?该怎么计算?int count = 0; for (int i = 0; i < N ; ++ i) { for (int j = 0; j < N ; ++ j) { ++count; } }这个循环是一个循环的嵌套, 执行次数是
N*N
for (int k = 0; k < 2 * N ; ++ k) { ++count; }这个循环就是一个普通的循环, 执行次数是
2*N
int M = 10; while (M--) { ++count; }这个循环是 可以确定次数的循环, 每次函数调用执行的次数是一定的, 执行次数是
10次
O(N^2 + 2*N + 10)
但是, 事实并不是这样的。
这个函数的时间复杂度 其实是 O(N^2)
为什么?N = 10, 执行次数: 10*10 + 2*10 + 10 = 130N = 100, 执行次数: 100*100 + 2*100 + 10 = 10210N = 1000, 执行次数: 1000*1000 + 2*1000 + 10 = 1002010N = 10000, 执行次数: 10000*10000 + 2*10000 + 10 = 100020010
N 的增大, 2*N + 10 在最终执行次数中的 占比越来越小 了, 也代表着 其对最终执行次数的 影响越来越小 了
2*N + 10 在结果中的占比: 23% -> 2% -> 0.2% -> 0.02%N 足够大的时候, 就已经可以忽略 2*N + 10 的影响了, 所以只需要计算 N^2 就能够代表函数的执行次数, 所以 函数 Fun2 的时间复杂度 其实是 O(N^2)。大 0 的渐进表示法大 O 的渐进表示法
大O符号(Big O notation): 是用于描述函数渐进 行为 的数学符号大O表示法 计算复杂度的方法一般有:- 基本操作的执行次数中, 相加的常数一般用
1取代 即:N^2 + 2*N + 10--->N^2 + 2*N + 1或:O(100)--->O(1), 即常数的时间复杂度, 均计算为O(1) - 在常数转后之后的执行次数函数中, 取最高次幂项作为时间复杂度,
即:
O(N^2 + 2*N + 1)--->O(N^2) - 如果转换后的执行次数函数中, 存在
最高次幂项 且 此项不为1, 则只保留单个此项作为时间复杂度(即放弃与其相乘的常数)即:O(4 * N^2)--->O(N^2)
去掉了那些对结果影响不大的项 , 简洁明了的表示出了时间复杂度。
所以 函数Fun2 的时间复杂度为: O(N^2) 忽略了 2*N + 10时间复杂度的最好、最坏、平均情况
//查找整型数组中第一个 10 的位置
int Find_10(int *arr, int arrSize)
{
int i = 0;
while(arrSize--)
{
if(*arr == 10)
{
return i;
}
arr++;
i++;
}
return -1;
}10 的位置, 但是 第一个 10 有可能出现在 一个数组中的任何位置, 甚至不出现在数组中。arr[0] arr[n - 1] arr[n / 2] , 被查找的数的位置是不定的, 所以 这个函数中 基本操作的执行次数也是不定的。一个算法的时间复杂度, 就用最坏情况下的复杂度来表示
Find_10 这个函数的时间复杂度, 实际就是 O(N)。
「PS:计算基本操作的执行次数, 结果中的未知数用 N 或 M 代表(只有一个未知数 用 N,两个未知数 用 N 和 M, 多个可以用其他)」
时间复杂度计算举例
// 计算Func1的时间复杂度? void Func1(int N) { int count = 0; for (int k = 0; k < 2 * N ; ++k) { ++count; } int M = 10; while (M--) { ++count; } printf("%d\n", count); }此函数, 通过分析 拥有两个循环体, 一个循环
2*N次, 另一个循环10次 按照 大O 渐进表示法, 时间复杂度为O(N)
// 计算Func2的时间复杂度? void Func2(int N, int M) { int count = 0; for (int k = 0; k < M; ++k) { ++count; } for (int k = 0; k < N ; ++ k) { ++count; } printf("%d\n", count); }此函数, 通过分析 拥有两个循环体, 一个循环
M次, 另一个循环N次 按照 大O 渐进表示法, 时间复杂度为O(M + N)
// 计算Func3的时间复杂度? void Func3(int N) { int count = 0; for (int k = 0; k < 100; ++k) { ++count; } printf("%d\n", count); }此函数, 通过分析 有一个循环体, 但是循环体循环次数与传入参数无关, 固定循环
100次 按照 大O 渐进表示法, 时间复杂度为O(1)
// 计算BubbleSort的时间复杂度? void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i-1] > a[i]) { Swap(&a[i-1], &a[i]); exchange = 1; } } if (exchange == 0) break; } }此函数为
冒泡排序(排升序)需要分情况分析: 最好的情况是: 除了第一位其他都已位升序, 则只需要循环N次, 即将第一位数据冒泡至最后一位最坏的情况是: 数据按照降序排列, 则每一个数据都要进行排序, 计算执行次数的结果为:(N*(N+1)/2次 按照 大O 渐进表示法, 取最坏的情况时间复杂度为O(N^2)
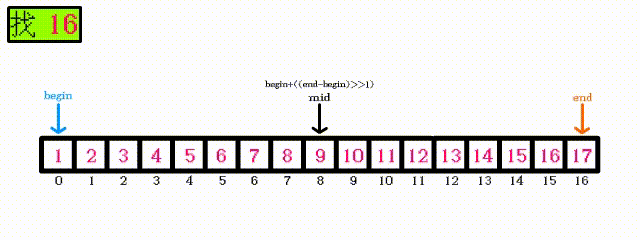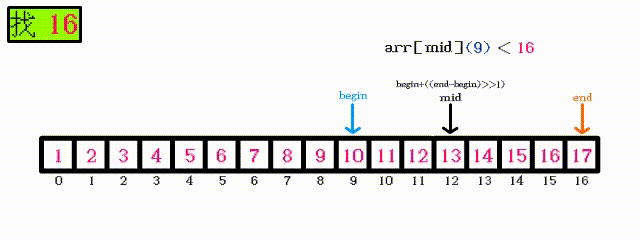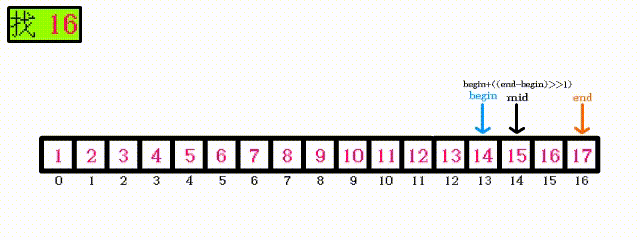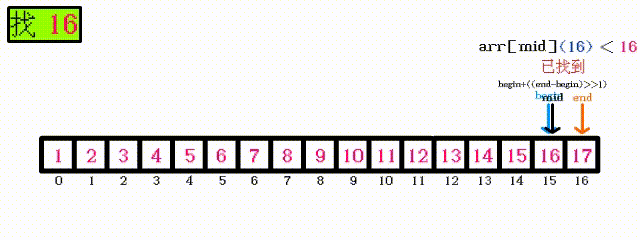
// 计算BinarySearch的时间复杂度? int BinarySearch(int* a, int n, int x) { assert(a); int begin = 0; int end = n-1; while (begin < end) { int mid = begin + ((end-begin)>>1); if (a[mid] < x) begin = mid+1; else if (a[mid] > x) end = mid; else return mid; } return -1; }此函数为
二分查找,(被查找的数据必须是有序的)同样需要分情况分析: 最好的情况:指定数据在数组中间位置, 只需要执行一次, 即第一次查找就查找到指定数据 最坏的情况:二分查找的原理:
因为使用二分查找的数据必须是有序的, 所以可以通过缩小查找范围来进行查找二分查找每次查找一次,下一次查找的范围会缩小为当前范围的一半只需要一张动图就可解释:可以看出, 每次查找之后, 下一次需要查找的元素只剩下一半, 所以最坏的情况其实是 需要查找:
log N次复杂度中, log N即为 以2为底N的对数所以按照 大O 渐进表示法, 取最坏的情况时间复杂度为
O(log N)
// 计算阶乘递归Fac的时间复杂度? long long Fac(size_t N) { if(0 == N) return 1; return Fac(N-1)*N; }此函数为
递归求阶乘递归求阶乘, 通过计算可以算出, 求N的阶乘则函数调用了N次 所以按照 大O 渐进表示法, 时间复杂度为O(N)
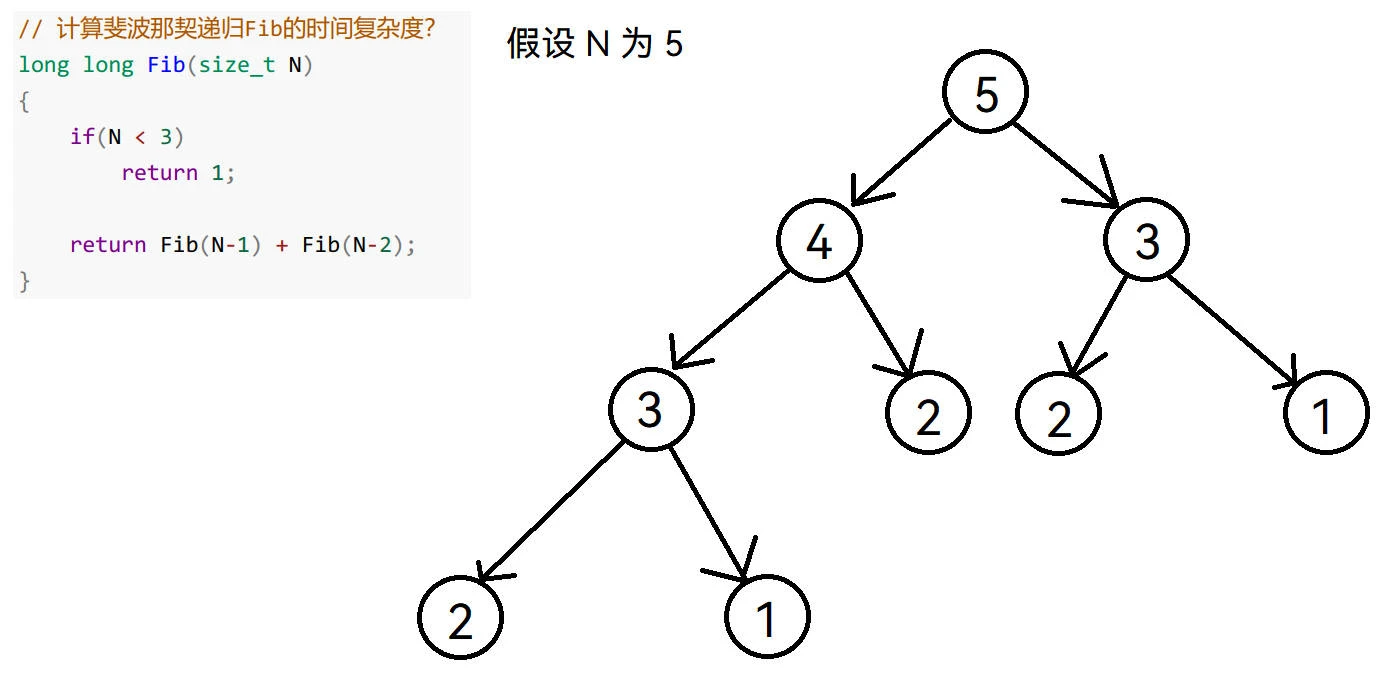
// 计算斐波那契递归Fib的时间复杂度 long long Fib(size_t N) { if(N < 3) return 1; return Fib(N-1) + Fib(N-2); }此函数为
递归求斐波那契数列递归求斐波那契数列, 一个简单的递归分析图:发现正常调用函数, 会再发生两次递归, 所以应该是
2^N但是因为当N < 3会返回1, 不再递归, 所以应该是2^N - x(不容易计算所以用 x 表示), 但是无论怎样, 相减的常数因该是对2^N造不成多大影响的 所以按照 大O 渐进表示法, 时间复杂度为O(2^N)
空间复杂度
空间复杂度 主要衡量一个算法运行所需要的额外空间额外空间额外空间 ?函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了, 在函数运行前就已经确定了一部分空间, 这些空间的占用不能由算法本身决定函数在运行时候申请的额外空间 来确定。这里推荐一篇 详细又简单 的 函数栈帧 的好文章:
在函数内使用动态开辟内存的函数, 以及创建柔性数组等操作, 就会增加函数的额外空间哦
空间复杂度 和 时间复杂度 的表示方法一样, 都用 大O渐进表示法。空间复杂度的计算举例
// 计算BubbleSort的空间复杂度? void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i-1] > a[i]) { Swap(&a[i-1], &a[i]); exchange = 1; } } if (exchange == 0) break; } }分析代码可以看出, 冒泡排序额外使用的空间并没有与
N发生关联。使用了常量个额外空间 所以 按照 大O 渐进表示法, 空间复杂度为O(1)
// 计算Fibonacci的空间复杂度? // 返回斐波那契数列的前n项 long long* Fibonacci(size_t n) { if(n==0) return NULL; long long * fibArray = (long long *)malloc((n+1) * sizeof(long long)); fibArray[0] = 0; fibArray[1] = 1; for (int i = 2; i <= n ; ++i) { fibArray[i] = fibArray[i - 1] + fibArray [i - 2]; } return fibArray; }这是使用
数组实现的计算斐波那契数列的 前N 项分析代码可以看出, 这段代码 使用
malloc函数开辟了n+1个long long类型的空间, 即额外使用的空间与N1:1相关所以 按照 大O 渐进表示法, 空间复杂度为
O(N)
// 计算阶乘递归Fac的空间复杂度? long long Fac(size_t N) { if(N == 0) return 1; return Fac(N-1)*N; }
递归求N的阶乘分析代码可以看出, 代码执行需要递归
N次, 且每次递归都需要开辟函数栈帧,每次函数栈帧开辟都会消耗常量个空间, 所以是常量 * N按照 大O 渐进表示法, 空间复杂度为
O(N)
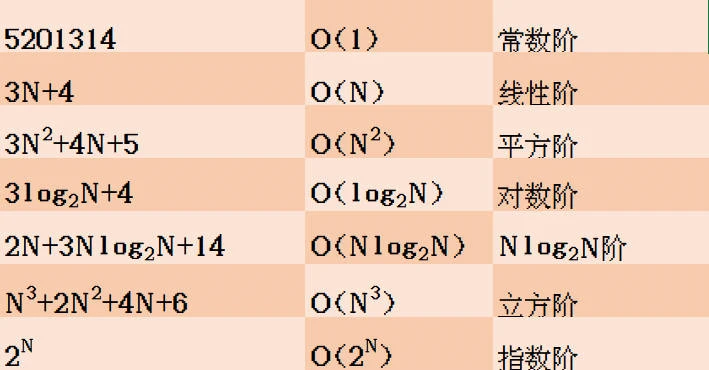
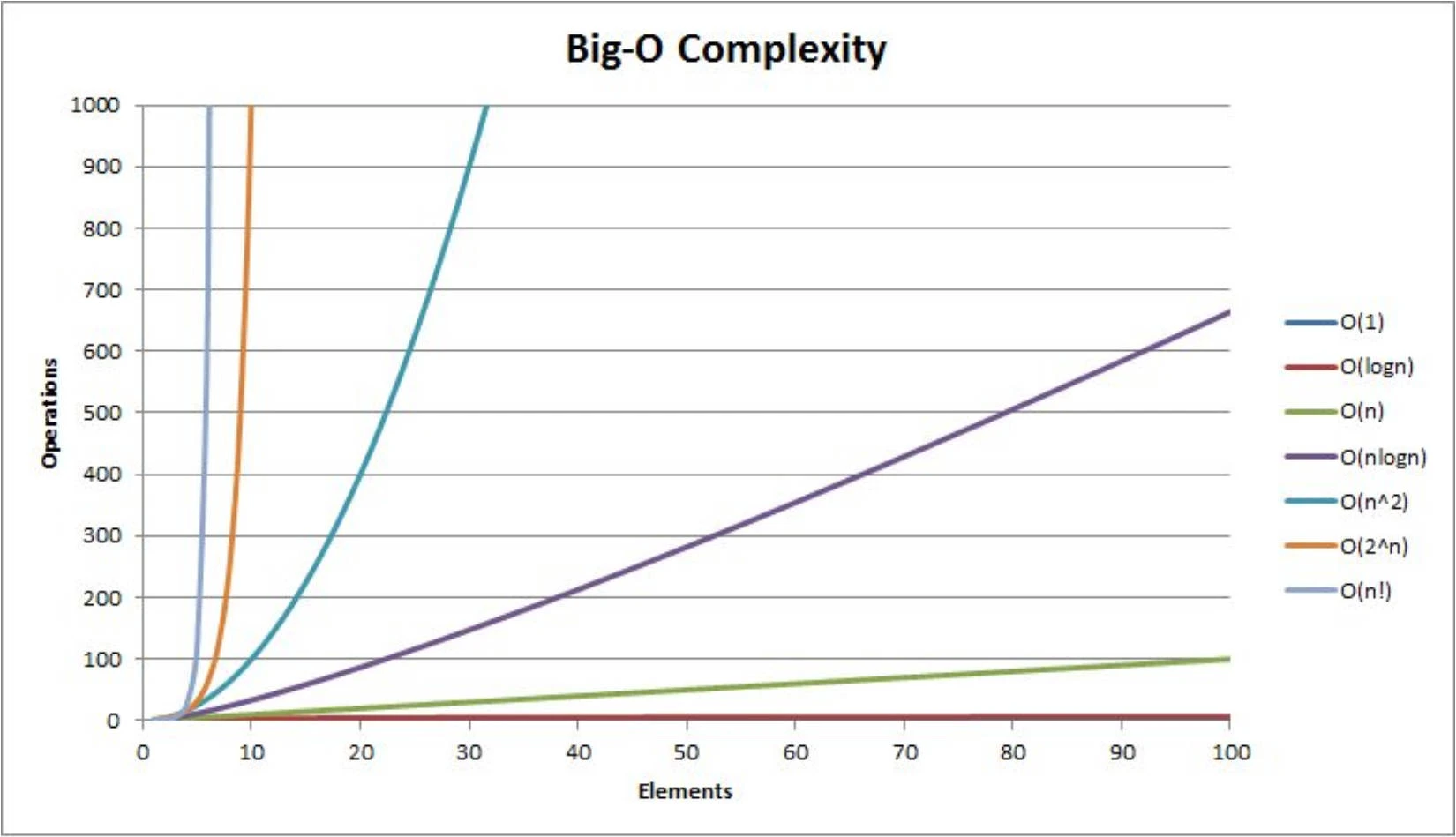
时间复杂度 和 空间复杂度 的介绍其实大部分的代码, 时间、空间复杂度是不容易直接看出来的, 一定要执行分析。对存在循环体的代码, 也不要直接简单粗暴的去数循环体执行的次数, 因为循环并不一定是都需要执行的。一定要分析复杂度对比
结束语
数据结构与算法 这片神秘海域的初探索向更深海域探索的重要基石
作者: 哈米d1ch 发表日期:2022 年 4 月 14 日