STL 2022 年 10 月 25 日

[C++-STL] set和map容器的模拟实现

STL容器中, set 和 map 虽然底层都是红黑树, 但是这两个容器的模板参数是不一样的, 这是一个非常需要解决的问题

STL 树容器约7908字 -- 阅读时间≈21分钟

set 和 map 模板参数

STL容器中, set 和 map 虽然底层都是红黑树, 但是这两个容器的模板参数是不一样的, 在只考虑数据类型的情况下：

set 是 template<class Key>

map 则是 template<class Key, class Value>

很明显, 两种容器的模板参数数量都是不同的

要如何解决相同的底层实现, 但是不同的模板参数呢？

有两种很简单粗暴的解决方法：

对set设计一个只有单个数据的红黑树; 对map设计一个两个数据类型的红黑树
设计一个两个数据类型的红黑树, 但是实现set时, 模板参数默认传0

但是这两种方法一个浪费, 一个粗暴，都不是那么的优秀

简单分析一下 STL源码是怎么解决这个问题的：

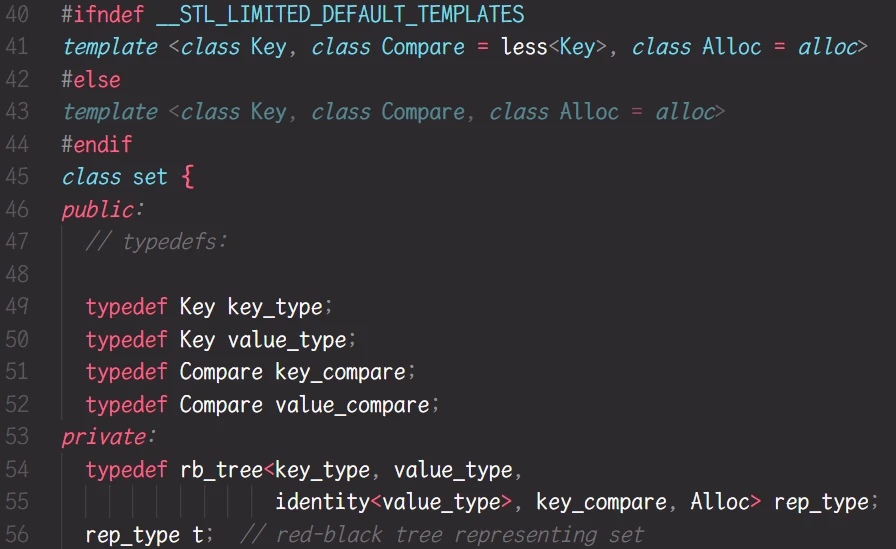
STL关于 set的部分源码：

可以看到, typedef红黑树的部分, 红黑树的模板参数传参是 <key_type, value_type>

而 key_type 和 value_type 其实都是 Key

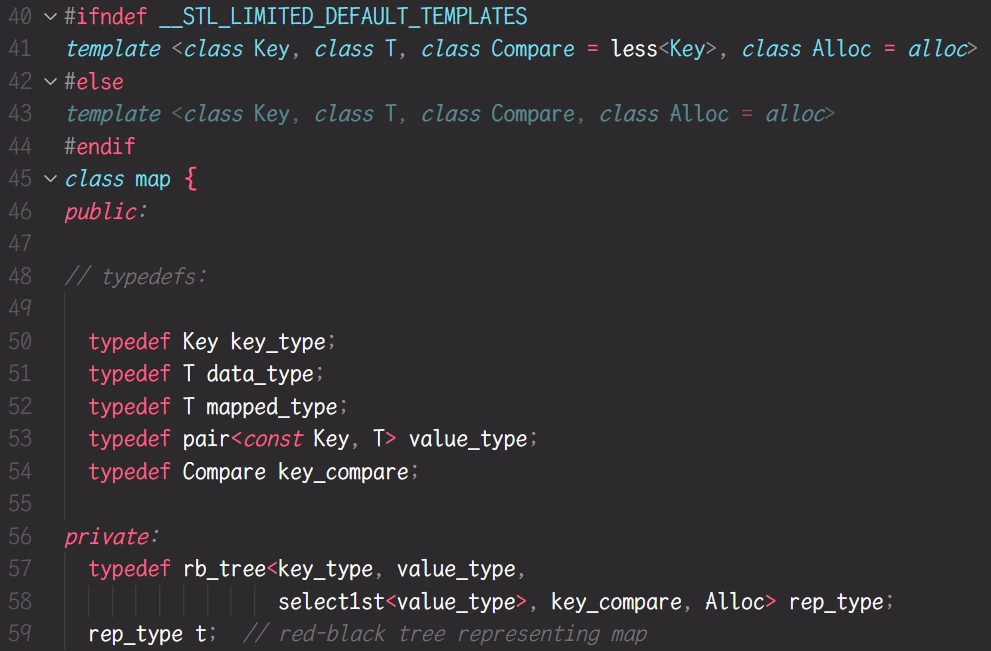
STL关于 map的部分源码:

map中 typedef红黑树的部分, 红黑树的模板参数传参也是 <key_type, value_type>

但是 map的 key_type 是 Key, 而 value_type 是 pair<const Key, T>

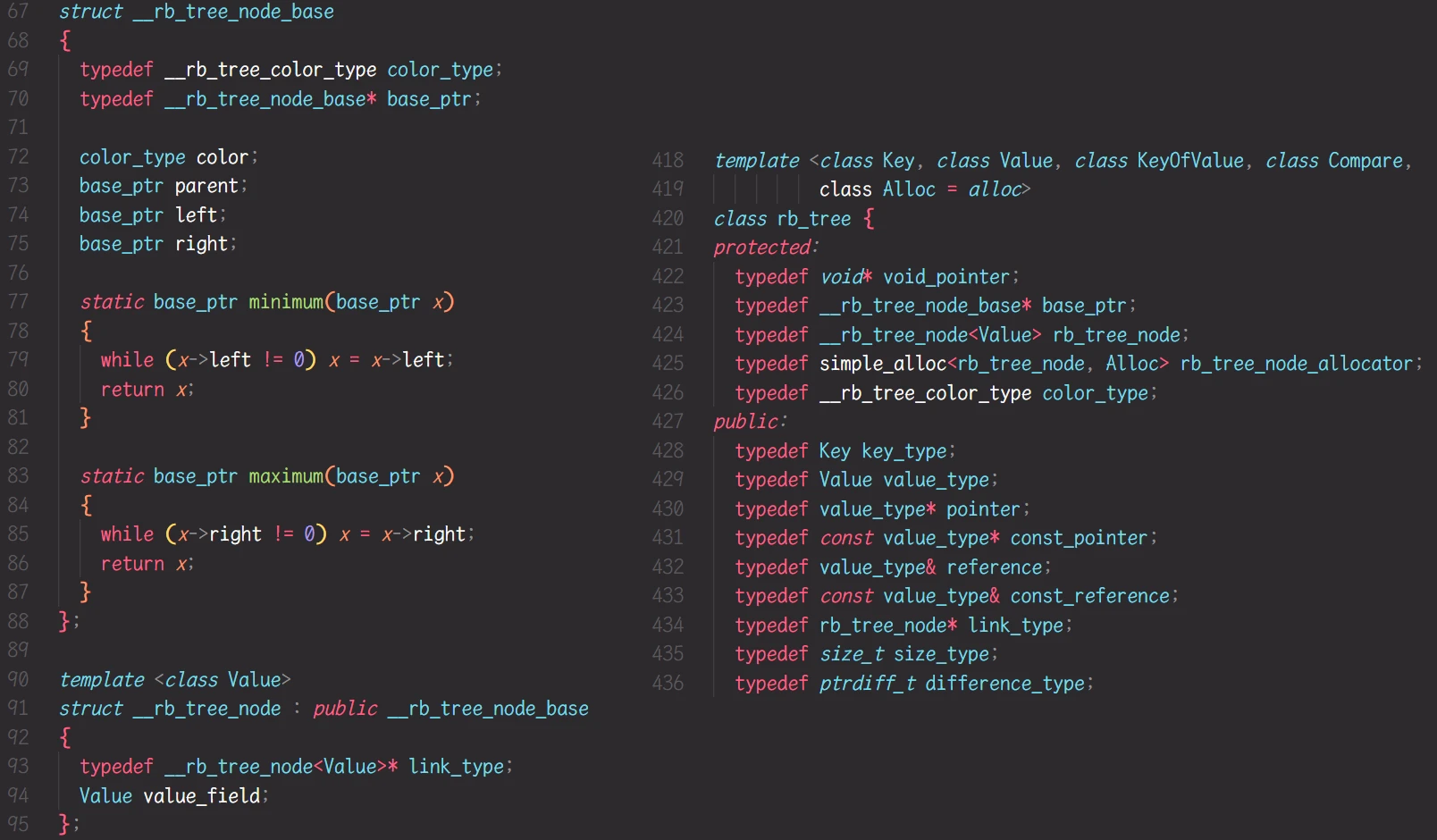
只看 set 和 map 类型的部分源码基本看不出什么, 只能看出 STL实现两容器底层使用的是有两个数据模板参数的红黑树

想要进一步看出具体的解决方案, 还要阅读一下红黑树的部分源码

STL关于红黑树的部分源码：

图中, 左半部分是关于红黑树节点的部分源码; 右半部分是关于红黑树结构的部分源码

阅读左半部分的源码, 可以发现 STL实现红黑树节点, 使用了继承：

将每个节点都具有的部分：颜色父亲左孩子右孩子定义为类 rb_tree_node_base; 定义另一个类只拥有一个Value类型的成员变量, 其他继承于子类

再阅读右半部分的源码, 发现 __rb_tree_node<Value> 被typedef为 rb_tree_node, 所以红黑树的节点其实是 __rb_tree_node<Value> 类型的

而 STL中 set 底层红黑树传入的模板参数是 <key_type, value_type>, 且这两个类型相同都是set的模板参数

map 底层红黑树传入的模板参数也是 <key_type, value_type>, 但是 map中的 value_type 是 pair<const Key, T>

总结一下：

STL实现set, set的关于数据的模板参数只有一个, 所以实例化 set 对象时使用set<Key>

set 底层由红黑树实现, 红黑树的数据模板参数有两个, set 内部的红黑树模板参数实际是 rb_tree<Key, Key>

STL实现map. map的关于数据的模板参数有两个, 所以实例化 map 对象时要 map<Key, T>

不过与 set不同, map底层红黑树的模板参数实际是 rb_tree<Key, pair<const Key, T>>

简单的分析过 STL关于set map rb_tree的这一部分源码后, 其实就可以发现：

set底层红黑树模板这样传参: rb_tree<Key, Key>, 红黑树节点中的数据类型是 Key; map底层红黑树模板这样传参: rb_tree<Key, pair<const Key, T>>, 红黑树节点中的数据类型是 pair<const Key, T>. 所以, 其实不难发现 STL中红黑树是以第二个模板参数的类型作数据类型来创建节点的

所以, 红黑树这样创建节点就不需要再区分 set 和 map 数据模板参数数目不同的问题, 因为

即使容器的数据模板参数再多, 在调用红黑树进行模板传参时 也需要将所有数据类型整合到一个类型中 作为红黑树的第二个模板参数进行传参

红黑树的实现

STL中红黑树节点的数据类型是红黑树的第二个模板参数的类型。所以, 此时实现的红黑树相较于上一篇文章分析红黑树时所写的红黑树结构就会有一定的区别：

// 枚举常量, 表示 红 黑
enum Color {
    RED,
    BLACK
};

template<class T>
struct RBTreeNode {
    RBTreeNode(const T& data = T())
        : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
        , _data(data)
        , _color(RED) 	// 新节点默认为红节点 
    {}

    RBTreeNode<T>* _pLeft;			// 节点左孩子
    RBTreeNode<T>* _pRight;		    // 节点右孩子
    RBTreeNode<T>* _pParent;		// 节点父亲节点

    T _data;					     // 节点数据
    Color _color;					// 节点颜色
};

template<class Key, class Value_type>
class RBTree {
    typedef RBTreeNode<Value_type> Node;			// 以 Value_type 作为节点类的模板参数 并 typedef

public:
    bool insert(const Value_type& data) {}

private:
    void rotateL(Node* parent) {}
    void rotateR(Node* parent) {}

    Node* _root = nullptr;
};

红黑树节点类模板，只有一个模板参数

红黑树类模板, 有两个数据类型模板参数, 但是只用第二个模板参数作节点的数据类型

红黑树节点数据的比较

红黑树是特殊的二叉搜索树, 所以在插入数据时是一定会比较节点的数据大小的

对于基本的数据类型, 直接使用 >、< 等比较运算符就可以了

但是对于复杂的类, 就比如 map 的节点数据类型 pair, 还可以直接使用 >、< 来实现目的吗？

pair类数据大小的比较

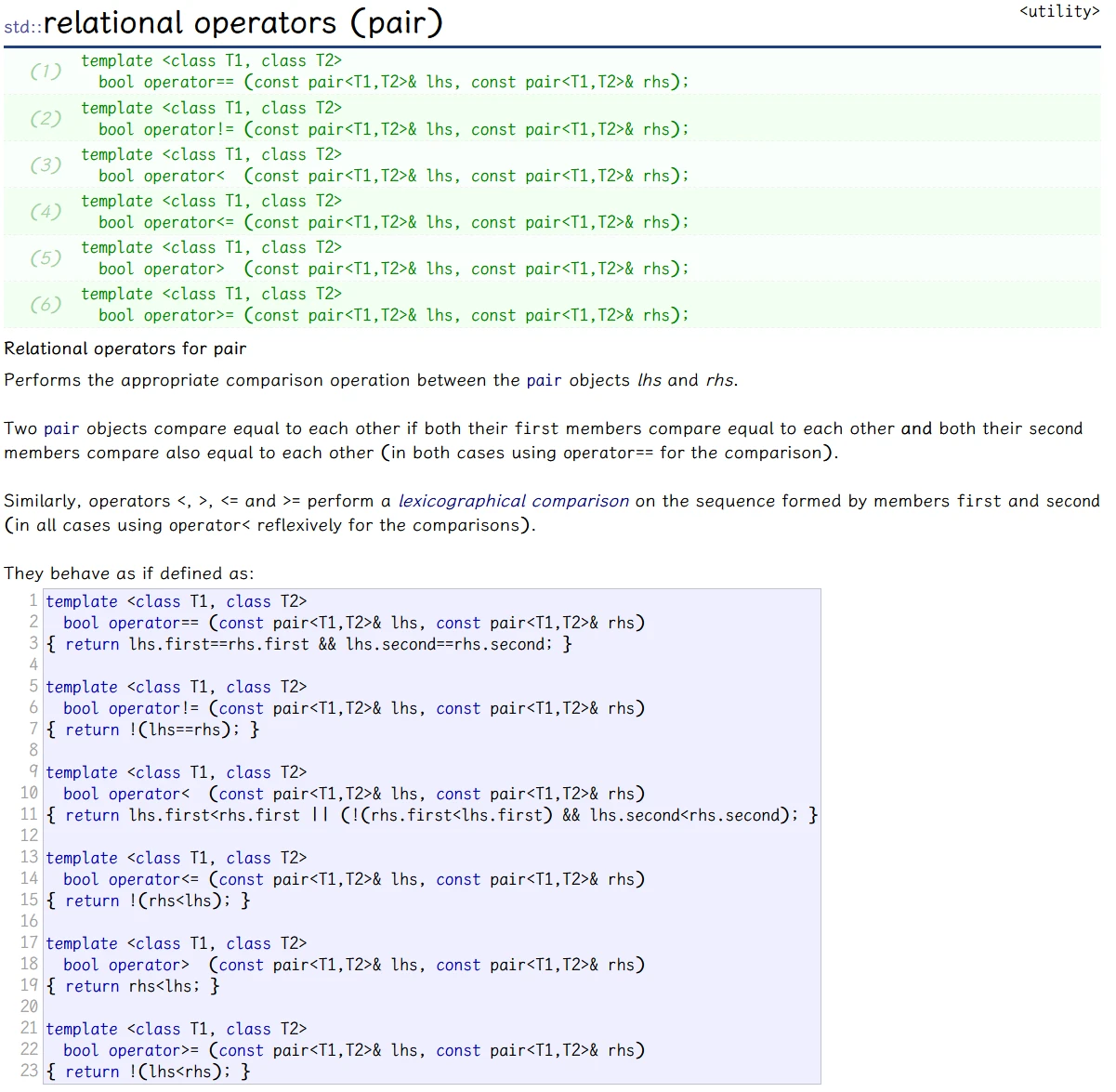
图中蓝紫色部分的代码就是 pair类中重载的比较运算符, 其中 == 和 < 运算符的功能是：

==: 两pair对象的 first 和 second 都相等, 则为真
<: 左pair 的first 小于右pair 的first 时 或 左pair的first 不小于右pair的first时, 且左pair的second 小于右pair的second时, 为真

可以发现, pair对象的比较与 pair对象的两个成员变量有关

红黑树第二个模板参数类型数据的比较

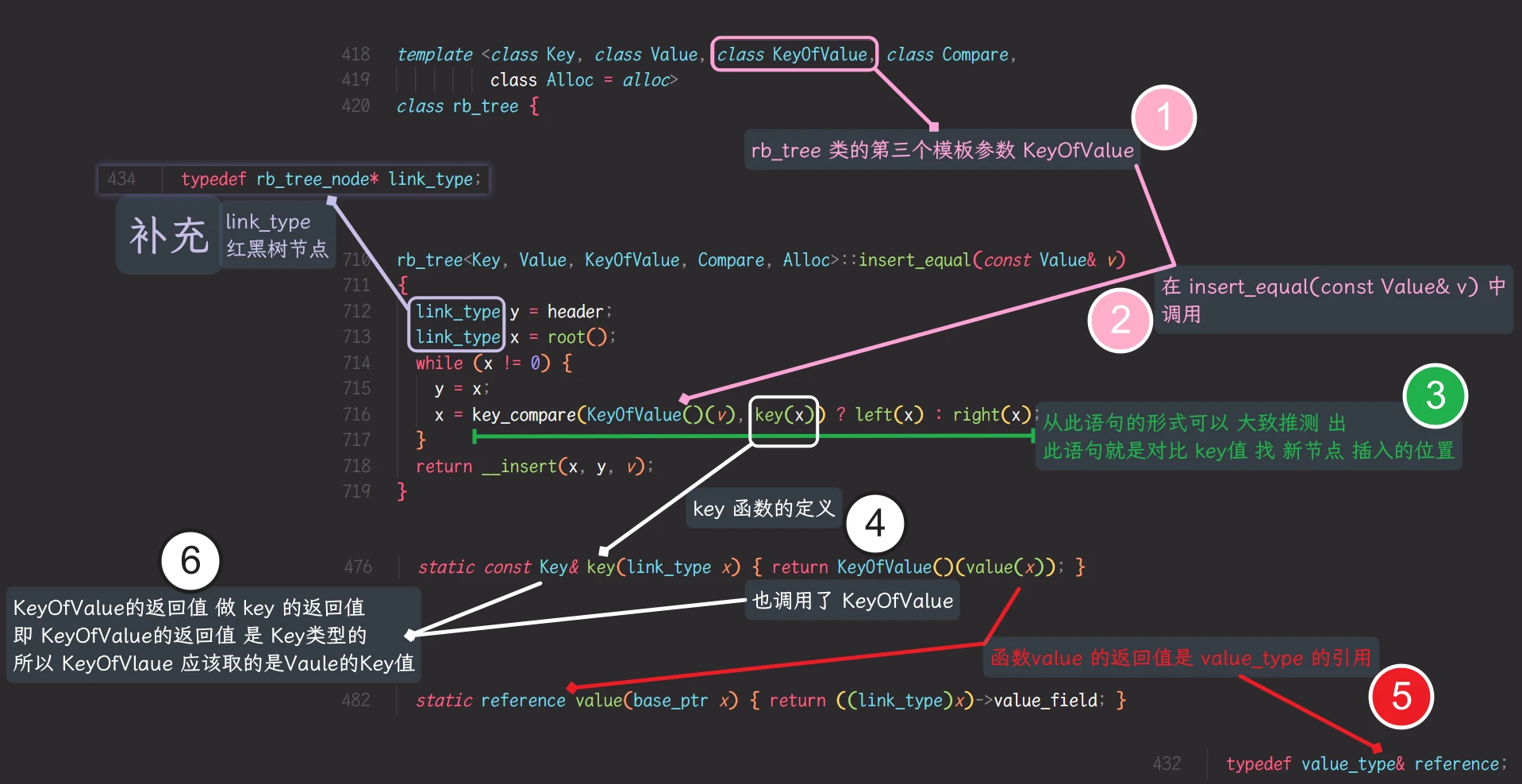
pair对象的比较与 pair对象的两个成员变量都有关系, 但是 红黑树中节点的比较应该只对比 Key 的值, 而不对比 T 的值

所以对set来说可以直接比较节点数据, 但是 对map来说不能直接比较节点数据, 因为 map节点数据的类型是 pair。

那么红黑树该如何设计, 才能兼容不同的容器呢？

其实可以效仿STL中的解决方法： 对不同的容器实现针对此容器的取节点Key值的 仿函数

这是在STL源码分析的部分关于 取节点数据的Key值的仿函数 的代码

所以, STL源码中 红黑树的第三个模板参数就是取节点数据的Key值的仿函数

仿函数需要在各自的容器中编写, 即在Set中写取set的Key值的仿函数, 在Map中写取Map的Key值的仿函数

set 的取key值的仿函数：

template<class Key>
class Set{
       struct SetKeyOfValue {
           const Key& operator() (const Key& key) {
               return key;
           }
       };
    };

在 Set类中定义一个私有仿函数

map 的取key值的仿函数：

template<class Key, class Value>
class Map{
       struct MapKeyOfValue {
           const Key& operator() (const pair<Key, Value>& kv) {
               return kv.first;
           }
       };
    };

Set、Map结构及底层红黑树插入实现

既然 Set和Map的底层红黑树 需要使用仿函数取对应的 key值, 所以此时的红黑树插入节点时, 无论是找位置还是调整节点都需要使用仿函数来操作：

// 枚举常量, 表示 红 黑
enum Color {
    RED,
    BLACK
};

template<class T>
struct RBTreeNode {
    // RedBlackTreeNode 红黑树节点
    RBTreeNode(const T& data = T())
        : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
        , _data(data)
        , _color(RED) 	// 新节点默认为红节点 
    {}

    RBTreeNode<T>* _pLeft;			// 节点左孩子
    RBTreeNode<T>* _pRight;		    // 节点右孩子
    RBTreeNode<T>* _pParent;		// 节点父亲节点

    T _data;					     // 节点数据
    Color _color;					// 节点颜色
};

template<class Key, class Value_type, class KeyOfValue>
class RB_Tree {
    typedef RBTreeNode<Value_type> Node;			// 对节点类型进行typedef

public:
    bool insert(const Value_type& data) {
        if (_root == nullptr) {
            // 树为空时, 插入新节点
            _root = new Node(data);
            _root->_color = BLACK;			// 根节点要为 黑

            return true;
        }
        
        KeyOfValue KOV;				// 实例化仿函数对象, 为调用仿函数
        
        // 树不为空, 就从根节点开始找位置
        Node* cur = _root;
        Node* parent = cur->_pParent;
        while (cur) {
            if (KOV(data) > KOV(cur->_data)) {		// 调用仿函数找key值 对比
                // 插入数据大, 就向右子树找
                parent = cur;
                cur = cur->_pRight;
            }
            else if (KOV(data) < KOV(cur->_data)) {
                // 插入数据小, 就向左子树找
                parent = cur;
                cur = cur->_pLeft;
            }
            else {
                // 树中已存在插入数据, 返回 false 插入失败
                return false;
            }
        }

        // 出循环之后, cur所在位置就是 新节点需要插入的位置
        cur = new Node(data);
        cur->_color = RED;
        // parent 与 cur连接起来
        if (KOV(data) > KOV(parent->_data)) {
            // 数据大, 即新节点是父亲节点的右节点
            parent->_pRight = cur;
        }
        else {
            // 数据小, 即新节点是父亲节点的左节点
            parent->_pLeft = cur;
        }
        cur->_pParent = parent;

        // 上面插入新节点时 已经记录了 cur 和 parent节点
        while (parent && parent->_color == RED) {
            // 父亲节点存在, 且父亲节点也为红色时
            Node* grandFa = parent->_pParent; 			// 记录祖先节点
            assert(grandFa);						 // 断言祖父节点存在
            // 如果祖父节点不存在, 就说明 parent节点是树的根, 是不可能的 因为红黑树根不可能是红色的

            if (parent == grandFa->_pLeft) {
                // 父亲节点是祖先节点的左孩子
                Node* uncle = grandFa->_pRight;			// 记录叔叔节点
                if (uncle && uncle->_color == RED) {
                    // 叔叔节点存在 且是红节点
                    parent->_color = uncle->_color = BLACK;			// 父亲节点 和 叔叔节点改为黑色
                    grandFa->_color = RED;						 // 祖父节点 改为红色

                    cur = grandFa;								// 更新 grandFa节点为新的cur节点
                    parent = cur->_pParent;						  // 更新 新的parent节点
                }
                else {
                    // uncle为空 或 为黑时
                    if (cur == parent->_pLeft) {
                        // parent是grandFa的左孩子, cur是parent的左孩子, 即 直线的情况
                        rotateR(grandFa);				// 将 祖先节点作为rotateR的parent, 右单旋

                        parent->_color = BLACK;			 // 更新 parent节点颜色为黑
                        grandFa->_color = RED;			 // 更新 grandFa节点颜色为红
                    }
                    else {
                        // parent是grandFa的左孩子, cur是parent的右孩子, 即 折线的情况
                        rotateL(parent);				// 先将 parent节点作为rotateL的parent, 左单旋
                        rotateR(grandFa); 				// 再将 grandFa节点作为rotateR的parent, 右单旋

                        cur->_color = BLACK;			// 更新 cur节点颜色为黑
                        grandFa->_color = RED;			// 更新 grandFa节点颜色为红
                    }
                    // 处理之后 结束循环
                    break;
                }
            }
            else {
                // 父亲节点是祖先节点的右孩子
                Node* uncle = grandFa->_pLeft;			// 记录叔叔节点
                if (uncle && uncle->_color == RED) {
                    parent->_color = uncle->_color = BLACK;
                    grandFa->_color = RED;

                    cur = grandFa;
                    parent = cur->_pParent;
                }
                else {
                    // uncle为空 或 为黑时
                    if (cur == parent->_pRight) {
                        // parent是grandFa的右孩子, cur是parent的右孩子, 即 直线的情况
                        rotateL(grandFa);				// 将 祖先节点作为rotateL的parent, 左单旋

                        parent->_color = BLACK;			 // 更新 parent节点颜色为黑
                        grandFa->_color = RED;			 // 更新 grandFa节点颜色为红
                    }
                    else {
                        // parent是grandFa的右孩子, cur是parent的左孩子, 即 折线的情况
                        rotateR(parent);				// 先将 parent节点作为rotateR的parent, 右单旋
                        rotateL(grandFa); 				// 再将 grandFa节点作为rotateL的parent, 左单旋

                        cur->_color = BLACK;			// 更新 cur节点颜色为黑
                        grandFa->_color = RED;			// 更新 grandFa节点颜色为红
                    }
                    // 处理之后 结束循环
                    break;
                }
            }
        }
        _root->_color = BLACK;				  // 无论如何 最后更新根节点的颜色为黑

        return true;						// 插入完成, 返回true
    }

private:
    Node* _root = nullptr;
};

除了对比key值需要使用仿函数之外, 没有什么需要注意的

然后就是 Set 和 Map的结构

上面分析过：

Set 的模板参数只有一个就是数据的类型, 内部调用红黑树, 模板传参就是 rb_tree<Key, Key>
Map 的模板参数有两个, 则内部调用红黑树, 模板传参就是 rb_tree<Key, pair<Key, Value>>

而由于需要兼容不同数据类型的指定方法的key值对比, 所以添加一个仿函数用来取key值, 所以 set 和 map 的结构定义：

Set 的结构：

template<class Key>
class Set {
	typedef Key key_type;
	typedef Key value_type;

	// 取key值的仿函数
	struct SetKeyOfValue {
		const key_type& operator() (const value_type& key) {
			return key;
		}
	};

private:
	RB_Tree<key_type, key_type, SetKeyOfValue> _tree;
};

Map 的结构：

template<class Key, class Value>
class Map {
	typedef Key key_type;
	typedef pair<Key, Value> value_type;		// pair<Key, Value>作为数据类型

	// 取key值的仿函数
	struct MapKeyOfValue {
		const key_type& operator() (const value_type& kv) {
			return kv.first;
		}
	};

private:
	RB_Tree<key_type, value_type, MapKeyOfValue> _tree;
};

* 红黑树的迭代器

红黑树是二叉树, 每个单位是一个节点, 所以红黑树迭代器应该与链表的迭代器相似成员变量是红黑树的节点

template<class Type, class Ref, class Ptr>			// 模板参数分别是 原类型，引用类型，指针类型
struct _RB_Tree_Iterator {
    typedef RBTreeNode<Type> Node;
    typedef _RB_Tree_Iterator<Typr, Ref, Ptr> Self;
    
    _RB_Tree_Iterator(Node* node)
        : _node(node)
    {}
    
    Ref operator*() {
        return _node->_data;					// * 解引用 返回节点中的数据。返回值是引用类型 因为需要提供修改功能
    }
    
    Ptr operator->() {
        return &_node->_data;					// & 取地址 返回节点中数据的地址。返回值是指针类型
    }
    
    // 可能需要其他类访问, 所以设置为公有的
    Node* _node;
};

红黑树的迭代器重要的不是结构, 最重要的是 ++ 和 -- 功能的逻辑和实现

迭代器 ++ — 的逻辑与实现

虽然红黑树的迭代器本质上就是树的某个节点, 但是由于其整体结构是一棵树, 所以 ++ -- 的功能并不能像链表那样直接控制前后节点，而是需要分析树的结构来进行功能的实现

set 和 map 的迭代器的 ++ 是 按照树的中序遍历顺序 移动的, 所以 rb_tree 的迭代器也需要按照此顺序

++

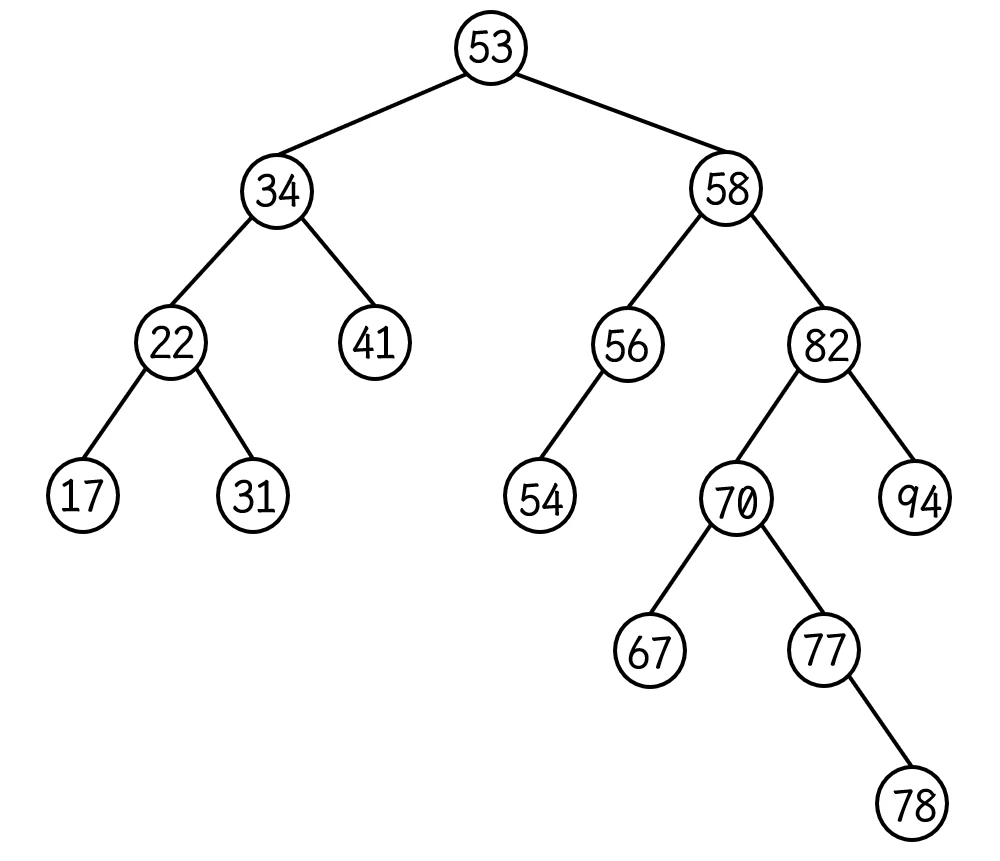
++ 操作需要将迭代器按照中序遍历的顺序移动, 怎么才能让指向当前节点位置的指针去指向中序遍历中下一个节点的位置呢？

以一棵二叉搜索树为例：

此红黑树的中序遍历是：17 22 31 34 41 53 54 56 58 67 70 77 78 82 94

所以迭代器实现的功能应该可以使迭代器++时按照此顺序进行移动, 即：

17节点 —> 22节点(17节点的父亲, 17节点是其左孩子);

22节点 —> 31节点(22节点的右孩子);

31节点 —> 34节点(31节点的祖父);

34节点 —> 41节点(34节点的右孩子);

41节点 —> 53节点(41节点的祖父);

53节点 —> 54节点(53节点的右子树的最左孩子);

54节点 —> 56节点(54节点的父亲, 54节点是其左孩子);

56节点 —> 58节点(56节点的父亲, 56节点是其左孩子);

58节点 —> 67节点(58节点的右子树的最左孩子);

67节点 —> 70节点(67节点的父亲, 67节点是其左孩子);

70节点 —> 77节点(70节点的右孩子);

77节点 —> 78节点(77节点的右孩子);

78节点 —> 82节点(78节点的父亲的祖父);

82节点 —> 94节点(82节点的右孩子);

经过分析可以发现：

当迭代器指向的节点处于某节点的左孩子时, 迭代器++, 迭代器就会指向 父亲节点:

17节点 —> 22节点(17节点的父亲, 17节点是其左孩子);

54节点 —> 56节点(54节点的父亲, 54节点是其左孩子);

56节点 —> 58节点(56节点的父亲, 56节点是其左孩子);

67节点 —> 70节点(67节点的父亲, 67节点是其左孩子);

这之中, 箭头左边的节点都是右边节点的左孩子

当迭代器所指节点拥有右子树时, 迭代器++, 迭代器就会指向 右子树的最左节点:

22节点 —> 31节点(22节点的右孩子);

34节点 —> 41节点(34节点的右孩子);

53节点 —> 54节点(53节点的右子树的最左孩子);

58节点 —> 67节点(58节点的右子树的最左孩子);

70节点 —> 77节点(70节点的右孩子);

77节点 —> 78节点(77节点的右孩子);

82节点 —> 94节点(82节点的右孩子);

其中 31节点只是22节点的右孩子, 41节点只是34节点的右孩子…… 这是因为 右子树中只有一个节点, 就是此节点的右孩子, 也可以看作是右子树的最左节点

当迭代器指向的节点是某节点的右孩子时, 迭代器++, 迭代器应该指向 此节点祖先节点的路径上第一个不为某节点右孩子的节点的父亲节点:

31节点 —> 34节点(31节点的祖父);

31节点是22节点的右孩子, 所以向上找到 22节点, 22节点是34节点的左孩子, 即 22节点是 31节点祖先路径上的第一个不是右孩子的节点, 所以迭代器需要指向 22节点的父亲节点

41节点 —> 53节点(41节点的祖父);

78节点 —> 82节点(78节点的父亲的祖父);

78节点是77节点的右孩子, 向上找到 77节点, 77节点又是 70节点的右孩子, 继续向上找 70节点, 70节点是82节点的左孩子, 即 70节点是 78祖先路径上的第一个不是右孩子的节点, 所以迭代器++ 需要指向 70节点的父亲节点, 82节点

但是其实 1 和 3 是同一种情况：

此节点向上所在的路径上第一个不是某节点右孩子的节点的父亲节点

所以, 一共有两种情况

当迭代器指向的节点没有右孩子时, 即表示 需要找此节点向上路径上第一个不是右孩子的节点的父亲节点

当迭代器指向的节点存在右孩子时, 即表示 需要找此节点右子树的最左节点

根据上面的分析就可以写出红黑树迭代器++操作的相关代码：

Self& operator++() {        // 无 int参数, 前置++
    if (_node->_pRight == nullptr) {        // 迭代器指向节点 没有 右孩子
        // 需要从此节点向上找 第一个不是右孩子的节点的父亲节点
        Node* cur = _node;
        Node* parent = cur->_pParent;

        while (parent && cur == parent->_pRight) {      // 当父亲节点存在, 且cur节点还是其右孩子时 循环继续
            cur = cur->_pParent;
            parent = parent->_pParent;
        }

        // 走到这里 cur节点就是 第一个不为右孩子的节点
        _node = parent;
        // 如果 迭代器++ 之前 指向的是树中最后一个节点, 则 执行上述代码之后
        // cur会走到 整棵树的根节点, 而根节点的parent为空
        // 所以 迭代器会为空
    }
    else {              // 迭代器指向的节点 存在右子树
        // 找右子树的最左节点
        Node* farLeft = _node->_pRight;
        while (farLeft->_pLeft) {
            farLeft = farLeft->_pLeft;
        }

        _node = farLeft;
    }

    return *this;                       // 返回新的迭代器
}

Self operator++(int) {                 // 后置++
    Self tmp(*this);                    // 拷贝此迭代器
    
    ++(*this);                          // 复用前置++

    return tmp;                         // 返回++前 拷贝的迭代器
}

—

++ 解决了之后, -- 就会非常的简单

与 ++ 的路径相反, 那么操作与 ++ 也相反就可以

Self& operator--()                          // 无 int参数 前置--
{
    if (_node->_left == nullptr) {          // 当迭代器指向的节点 不存在左孩子 时
        // 需要从此节点向上找 第一个不是左孩子 的节点的父亲节点
        Node* cur = _node;
        Node* parent = cur->_pParent;
        
        while (parent && cur == parent->_pLeft) {
            cur = cur->_pParent;
            parent = parent->_pParent;
        }
        
        // 走到这里 cur节点就是 第一个不为左孩子的节点
        _node = parent;
    }
    else {               // 迭代器指向节点 存在 左孩子时
        // 找左子树的最右节点
        Node* subRight = _node->_pLeft;
        while (subRight->_pRight) {
            subRight = subRight->_pRight;
        }

        _node = subRight;
    }
    
    return *this;
}

Self operator--(int) {
    Self tmp(*this);

    --(*this);

    return tmp;
}

迭代器相关代码

++ 和 -- 介绍过之后, 红黑树迭代器最重要的内容就已经介绍完了, 剩下的就是补齐迭代器相等和不等比较的功能

template<class Type, class Ref, class Ptr>			// 模板参数分别是 原类型，引用类型，指针类型
struct _RB_Tree_Iterator {
    typedef RBTreeNode<Type> Node;
    typedef _RB_Tree_Iterator<Typr, Ref, Ptr> Self;

    _RB_Tree_Iterator(Node* node)
        : _node(node)
    {}

    Ref operator*() {
        return _node->_data;					// * 解引用 返回节点中的数据。返回值是引用类型 因为需要提供修改功能
    }

    Ptr operator->() {
        return &_node->_data;					// & 取地址 返回节点中数据的地址。返回值是指针类型
    }
    
    Self& operator++() {        // 无 int参数, 前置++
        if (_node->_pRight == nullptr) {        // 迭代器指向节点 没有 右孩子
            // 需要从此节点向上找 第一个不是右孩子的节点的父亲节点
            Node* cur = _node;
            Node* parent = cur->_pParent;

            while (parent && cur == parent->_pRight) {      // 当父亲节点存在, 且cur节点还是其右孩子时 循环继续
                cur = cur->_pParent;
                parent = parent->_pParent;
            }

            // 走到这里 cur节点就是 第一个不为右孩子的节点
            _node = parent;
            // 如果 迭代器++ 之前 指向的是树中最后一个节点, 则 执行上述代码之后
            // cur会走到 整棵树的根节点, 而根节点的parent为空
            // 所以 迭代器会为空
        }
        else {              // 迭代器指向的节点 存在右子树
            // 找右子树的最左节点
            Node* farLeft = _node->_pRight;
            while (farLeft->_pLeft) {
                farLeft = farLeft->_pLeft;
            }

            _node = farLeft;
        }

        return *this;                       // 返回新的迭代器
    }

    Self& operator++(int) {                 // 后置++
        Self tmp(*this);                    // 拷贝此迭代器

        ++(*this);                          // 复用前置++

        return tmp;                         // 返回++前 拷贝的迭代器
    }

    Self& operator--() {                     // 无 int参数 前置--
        if (_node->_left == nullptr) {          // 当迭代器指向的节点 不存在左孩子 时
            // 需要从此节点向上找 第一个不是左孩子 的节点的父亲节点
            Node* cur = _node;
            Node* parent = cur->_pParent;

            while (parent && cur == parent->_pLeft) {
                cur = cur->_pParent;
                parent = parent->_pParent;
            }

            // 走到这里 cur节点就是 第一个不为左孩子的节点
            _node = parent;
        }
        else {               // 迭代器指向节点 存在 左孩子时
            // 找左子树的最右节点
            Node* subRight = _node->_pLeft;
            while (subRight->_pRight) {
                subRight = subRight->_pRight;
            }

            _node = subRight;
        }

        return *this;
    }

    Self& operator--(int) {
        Self tmp(*this);

        --(*this);

        return tmp;
    }

    bool operator!=(const Self& It) const {
        return _node != It._node;
    }

    bool operator==(const Self& It) const {
        return _node == It._node;
    }

    // 可能需要其他类访问, 所以设置为公有的
    Node* _node;
};

底层红黑树实现

迭代器分析完毕之后, 就可以简单完善一下红黑树的接口了：

// 枚举常量, 表示 红 黑
enum Color {
    RED,
    BLACK
};

template<class T>
struct RBTreeNode {
    // RedBlackTreeNode 红黑树节点
    RBTreeNode(const T& data = T())
        : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
        , _data(data)
        , _color(RED) 	// 新节点默认为红节点 
    {}

    RBTreeNode<T>* _pLeft;			// 节点左孩子
    RBTreeNode<T>* _pRight;		    // 节点右孩子
    RBTreeNode<T>* _pParent;		// 节点父亲节点

    T _data;					     // 节点数据
    Color _color;					// 节点颜色
};

template<class Type, class Ref, class Ptr>			// 模板参数分别是 原类型，引用类型，指针类型
struct _RB_Tree_Iterator {
    typedef RBTreeNode<Type> Node;
    typedef _RB_Tree_Iterator<Type, Ref, Ptr> Self;

    _RB_Tree_Iterator(Node* node)
        : _node(node)
    {}

    Ref operator*() {
        return _node->_data;					// * 解引用 返回节点中的数据。返回值是引用类型 因为需要提供修改功能
    }

    Ptr operator->() {
        return &_node->_data;					// -> 返回节点中数据的地址。返回值是指针类型
    }
    
    Self& operator++() {        // 无 int参数, 前置++
        if (_node->_pRight == nullptr) {        // 迭代器指向节点 没有 右孩子
            // 需要从此节点向上找 第一个不是右孩子的节点的父亲节点
            Node* cur = _node;
            Node* parent = cur->_pParent;

            while (parent && cur == parent->_pRight) {      // 当父亲节点存在, 且cur节点还是其右孩子时 循环继续
                cur = cur->_pParent;
                parent = parent->_pParent;
            }

            // 走到这里 cur节点就是 第一个不为右孩子的节点
            _node = parent;
            // 如果 迭代器++ 之前 指向的是树中最后一个节点, 则 执行上述代码之后
            // cur会走到 整棵树的根节点, 而根节点的parent为空
            // 所以 迭代器会为空
        }
        else {              // 迭代器指向的节点 存在右子树
            // 找右子树的最左节点
            Node* farLeft = _node->_pRight;
            while (farLeft->_pLeft) {
                farLeft = farLeft->_pLeft;
            }

            _node = farLeft;
        }

        return *this;                       // 返回新的迭代器
    }

    Self& operator++(int) {                 // 后置++
        Self tmp(*this);                    // 拷贝此迭代器

        ++(*this);                          // 复用前置++

        return tmp;                         // 返回++前 拷贝的迭代器
    }

    Self& operator--() {                     // 无 int参数 前置--
        if (_node->_left == nullptr) {          // 当迭代器指向的节点 不存在左孩子 时
            // 需要从此节点向上找 第一个不是左孩子 的节点的父亲节点
            Node* cur = _node;
            Node* parent = cur->_pParent;

            while (parent && cur == parent->_pLeft) {
                cur = cur->_pParent;
                parent = parent->_pParent;
            }

            // 走到这里 cur节点就是 第一个不为左孩子的节点
            _node = parent;
        }
        else {               // 迭代器指向节点 存在 左孩子时
            // 找左子树的最右节点
            Node* subRight = _node->_pLeft;
            while (subRight->_pRight) {
                subRight = subRight->_pRight;
            }

            _node = subRight;
        }

        return *this;
    }

    Self& operator--(int) {
        Self tmp(*this);

        --(*this);

        return tmp;
    }

    bool operator!=(const Self& It) const {
        return _node != It._node;
    }

    bool operator==(const Self& It) const {
        return _node == It._node;
    }

    // 可能需要其他类访问, 所以设置为公有的
    Node* _node;
};

template<class Key, class Value_type, class KeyOfValue>
class RB_Tree {
    typedef RBTreeNode<Value_type> Node;			// 对节点类型进行typedef

public:
    // 由于需要在类外使用  所以 typedef 为公共的
    typedef _RB_Tree_Iterator<Value_type, Value_type&, Value_type*> iterator;
    typedef _RB_Tree_Iterator<Value_type, const Value_type&, const Value_type*> const_iterator;

    iterator begin() {          // begin 取树的最左节点
        Node* farLeft = _root;
        while (farLeft && farLeft->_pLeft) {
            // 判断 farLeft是否存在 是为了防止 树为空时 farLeft->_pLeft 访问使用空指针
            farLeft = farLeft->_pLeft;
        }

        return iterator(farLeft);
    }
    iterator end() {
        return iterator(nullptr);
    }

    const_iterator begin() const {
        Node* farLeft = _root;
        while (farLeft && farLeft->_pLeft) {
            farLeft = farLeft->_pLeft;
        }

        return const_iterator(farLeft);
    }
    const_iterator end() const {
        return const_iterator(nullptr);
    }

    iterator find(const Key& key) {
        //  查找节点 是按照 key 来找的
        Node* cur = _root;
        KeyOfValue KOV;
        while (cur) {
            if (KOV(cur->_data) < key) {
                cur = cur->_pRight;
            }
            else if (KOV(cur->_data) > key) {
                cur = cur->_pLeft;
            }
            else {
                return iterator(cur);
            }
        }

        return end();           // 走到这 就没有找到
    }
       
    // 插入数据之后 要返回新节点的迭代器 和 插入结果
    pair<iterator, bool> insert(const Value_type& data) {
        if (_root == nullptr) {
            // 树为空时, 插入新节点
            _root = new Node(data);
            _root->_color = BLACK;			// 根节点要为 黑

            return make_pair(iterator(_root), true);
        }
        
        KeyOfValue KOV;
        // 树不为空, 就从根节点开始找位置
        Node* cur = _root;
        Node* parent = cur->_pParent;
        while (cur) {
            if (KOV(data) > KOV(cur->_data)) {
                // 插入数据大, 就向右子树找
                parent = cur;
                cur = cur->_pRight;
            }
            else if (KOV(data) < KOV(cur->_data)) {
                // 插入数据小, 就向左子树找
                parent = cur;
                cur = cur->_pLeft;
            }
            else {
                // 树中已存在插入数据, 返回 false 插入失败
                return make_pair(iterator(cur), false);
            }
        }

        // 出循环之后, cur所在位置就是 新节点需要插入的位置
        cur = new Node(data);

        Node* newNode = cur;                // 记录新节点位置 以返回

        cur->_color = RED;
        // parent 与 cur连接起来
        if (KOV(data) > KOV(parent->_data)) {
            // 数据大, 即新节点是父亲节点的右节点
            parent->_pRight = cur;
        }
        else {
            // 数据小, 即新节点是父亲节点的左节点
            parent->_pLeft = cur;
        }
        cur->_pParent = parent;

        // 上面插入新节点时 已经记录了 cur 和 parent节点
        while (parent && parent->_color == RED) {
            // 父亲节点存在, 且父亲节点也为红色时
            Node* grandFa = parent->_pParent; 			// 记录祖先节点
            assert(grandFa);						 // 断言祖父节点存在
            // 如果祖父节点不存在, 就说明 parent节点是树的根, 是不可能的 因为红黑树根不可能是红色的

            if (parent == grandFa->_pLeft) {
                // 父亲节点是祖先节点的左孩子
                Node* uncle = grandFa->_pRight;			// 记录叔叔节点
                if (uncle && uncle->_color == RED) {
                    // 叔叔节点存在 且是红节点
                    parent->_color = uncle->_color = BLACK;			// 父亲节点 和 叔叔节点改为黑色
                    grandFa->_color = RED;						 // 祖父节点 改为红色

                    cur = grandFa;								// 更新 grandFa节点为新的cur节点
                    parent = cur->_pParent;						  // 更新 新的parent节点
                }
                else {
                    // uncle为空 或 为黑时
                    if (cur == parent->_pLeft) {
                        // parent是grandFa的左孩子, cur是parent的左孩子, 即 直线的情况
                        rotateR(grandFa);				// 将 祖先节点作为rotateR的parent, 右单旋

                        parent->_color = BLACK;			 // 更新 parent节点颜色为黑
                        grandFa->_color = RED;			 // 更新 grandFa节点颜色为红
                    }
                    else {
                        // parent是grandFa的左孩子, cur是parent的右孩子, 即 折线的情况
                        rotateL(parent);				// 先将 parent节点作为rotateL的parent, 左单旋
                        rotateR(grandFa); 				// 再将 grandFa节点作为rotateR的parent, 右单旋

                        cur->_color = BLACK;			// 更新 cur节点颜色为黑
                        grandFa->_color = RED;			// 更新 grandFa节点颜色为红
                    }
                    // 处理之后 结束循环
                    break;
                }
            }
            else {
                // 父亲节点是祖先节点的右孩子
                Node* uncle = grandFa->_pLeft;			// 记录叔叔节点
                if (uncle && uncle->_color == RED) {
                    parent->_color = uncle->_color = BLACK;
                    grandFa->_color = RED;

                    cur = grandFa;
                    parent = cur->_pParent;
                }
                else {
                    // uncle为空 或 为黑时
                    if (cur == parent->_pRight) {
                        // parent是grandFa的右孩子, cur是parent的右孩子, 即 直线的情况
                        rotateL(grandFa);				// 将 祖先节点作为rotateL的parent, 左单旋

                        parent->_color = BLACK;			 // 更新 parent节点颜色为黑
                        grandFa->_color = RED;			 // 更新 grandFa节点颜色为红
                    }
                    else {
                        // parent是grandFa的右孩子, cur是parent的左孩子, 即 折线的情况
                        rotateR(parent);				// 先将 parent节点作为rotateR的parent, 右单旋
                        rotateL(grandFa); 				// 再将 grandFa节点作为rotateL的parent, 左单旋

                        cur->_color = BLACK;			// 更新 cur节点颜色为黑
                        grandFa->_color = RED;			// 更新 grandFa节点颜色为红
                    }
                    // 处理之后 结束循环
                    break;
                }
            }
        }
        _root->_color = BLACK;				  // 无论如何 最后更新根节点的颜色为黑

        return make_pair(iterator(newNode), true);
    }

private:
    void rotateL(Node* parent) {
        Node* subR = parent->_pRight;
        Node* subRL = subR->_pLeft;

        parent->_pRight = subRL;
        if (subRL)
            subRL->_pParent = parent;

        Node* ppNode = parent->_pParent;

        subR->_pLeft = parent;
        parent->_pParent = subR;

        if (parent == _root) {
            _root = subR;
            _root->_pParent = nullptr;
        }
        else {
            if (parent == ppNode->_pLeft)
                ppNode->_pLeft = subR;
            else
                ppNode->_pRight = subR;

            subR->_pParent = ppNode;
        }
    }

    void rotateR(Node* parent) {
        Node* subL = parent->_pLeft;
        Node* subLR = subL->_pRight;

        parent->_pLeft = subLR;
        if (subLR)
            subLR->_pParent = parent;

        Node* ppNode = parent->_pParent;

        subL->_pRight = parent;
        parent->_pParent = subL;

        if (parent == _root) {
            _root = subL;
            _root->_pParent = nullptr;
        }
        else {
            if (parent == ppNode->_pLeft)
                ppNode->_pLeft = subL;
            else
                ppNode->_pRight = subL;

            subL->_pParent = ppNode;
        }
    }

    Node* _root = nullptr;
};

set 和 map 的封装

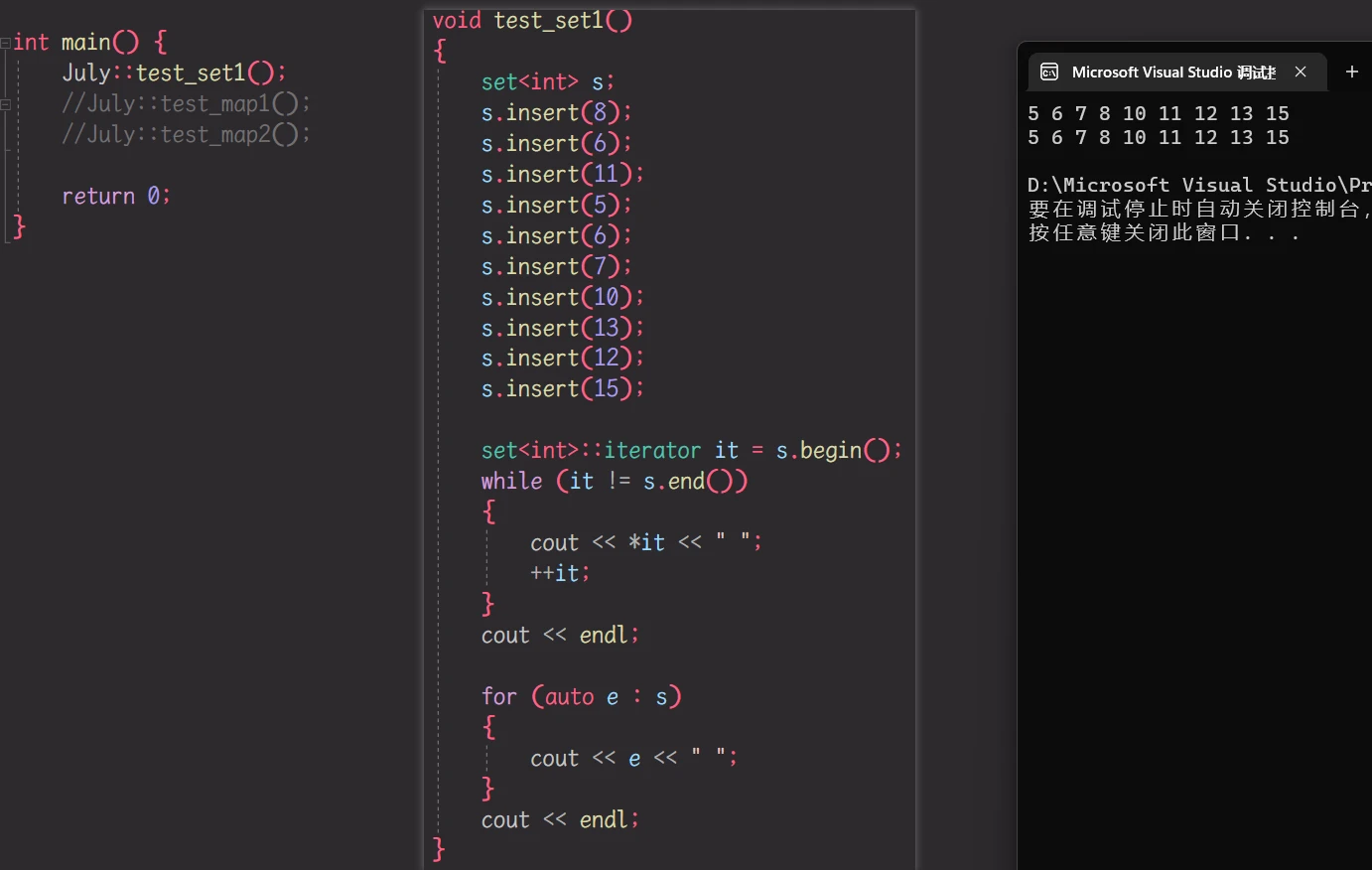
set 和 map 是以红黑树为底层封装起来的, 上面已经实现了红黑树的一些简单的接口的相关代码, 所以 set和map 的封装可以直接调用红黑树的接口进行实现：

set 的封装：

template<class Key>
class set {
	typedef Key key_type;
	typedef Key value_type;

	// 取key值的仿函数
	struct SetKeyOfValue {
		const key_type& operator() (const value_type& key) {
			return key;
		}
	};

public:
	// 封装红黑树的迭代器
	typedef typename RB_Tree<key_type, value_type, SetKeyOfValue>::const_iterator iterator;
	typedef typename RB_Tree<key_type, value_type, SetKeyOfValue>::const_iterator const_iterator;
	// 由于 迭代器需要在类外定义 所以需要typedef为 公用的

	iterator begin() const {
		return _tree.begin();
	}

	iterator end() const {
		return _tree.end();
	}

	pair<iterator, bool> insert(const value_type& v) {
		auto ret = _tree.insert(v);

		return pair<iterator, bool>(iterator(ret.first._node), ret.second);
	}

	iterator find(const key_type& key) {
		return _tree.find(key);
	}

private:
	RB_Tree<key_type, value_type, SetKeyOfValue> _tree;
};

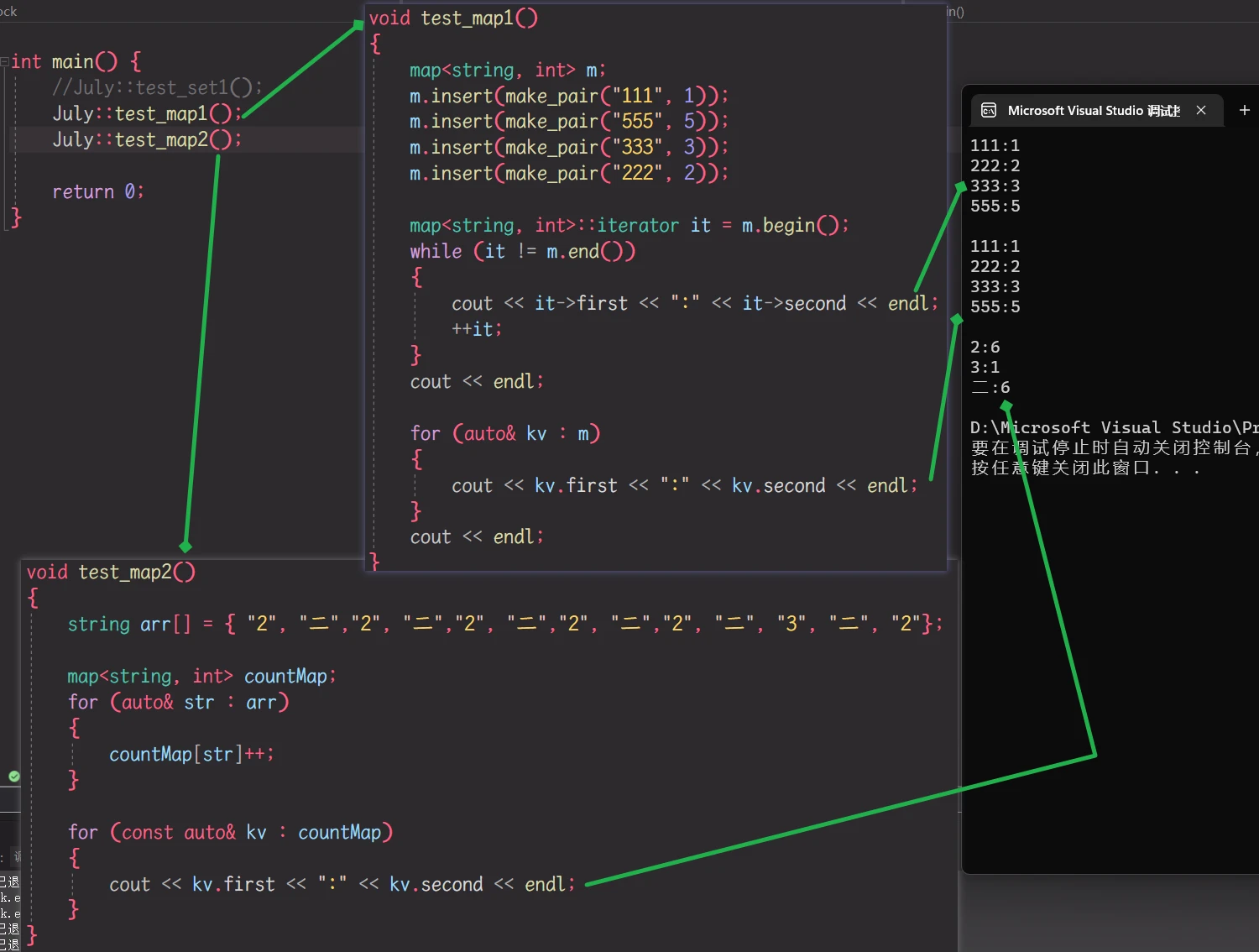
map 的封装：

template<class Key, class Value>
class map {
	typedef Key key_type;
	typedef pair<Key, Value> value_type;		// pair<Key, Value>作为数据类型

	// 取key值的仿函数
	struct MapKeyOfValue {
		const key_type& operator() (const value_type& kv) {
			return kv.first;
		}
	};

public:
	// 封装红黑树的迭代器
	typedef typename RB_Tree<key_type, value_type, MapKeyOfValue>::iterator iterator;
	typedef typename RB_Tree<key_type, value_type, MapKeyOfValue>::const_iterator const_iterator;

	iterator begin() {
		return _tree.begin();
	}

	iterator end() {
		return _tree.end();
	}

	pair<iterator, bool> insert(const value_type& kv) {
		return _tree.insert(kv);
	}

	iterator find(const key_type& k) {
		return _tree.find(k);
	}

	Value& operator[](const key_type& k) {
		pair<iterator, bool> ret = insert(make_pair(k, Value()));				// 调用map的插入

		return ret.first->second;
		// ret 的 first 是 map的迭代器
		// 红黑树中实现过 迭代器的 -> 操作是取 迭代器所指向节点的数据
		// map的数据是 pair<key_type, value_type> 类型的
		// 所以 ret.first->second 即为结果
	}

private:
	RB_Tree<key_type, value_type, MapKeyOfValue> _tree;
};

封装完成之后, 就可以进行测试：

测试 set：

测试 map：

作者：哈米d1ch 发表日期：2022 年 10 月 25 日