[C++-STL] 哈希表以及unordered_set和unordered_set的介绍
set和map之后, STL 之中还有两个名字与之非常相似的容器, unordered_set和unordered_mapset和map的底层是由红黑树实现的, 而unordered_set和unordered_map的底层是由 哈希表实现的- 第一部分: 简单的介绍
unordered_set和unordered_map - 第二部分: 分析、实现线性探测的哈希表
STL的哈希表

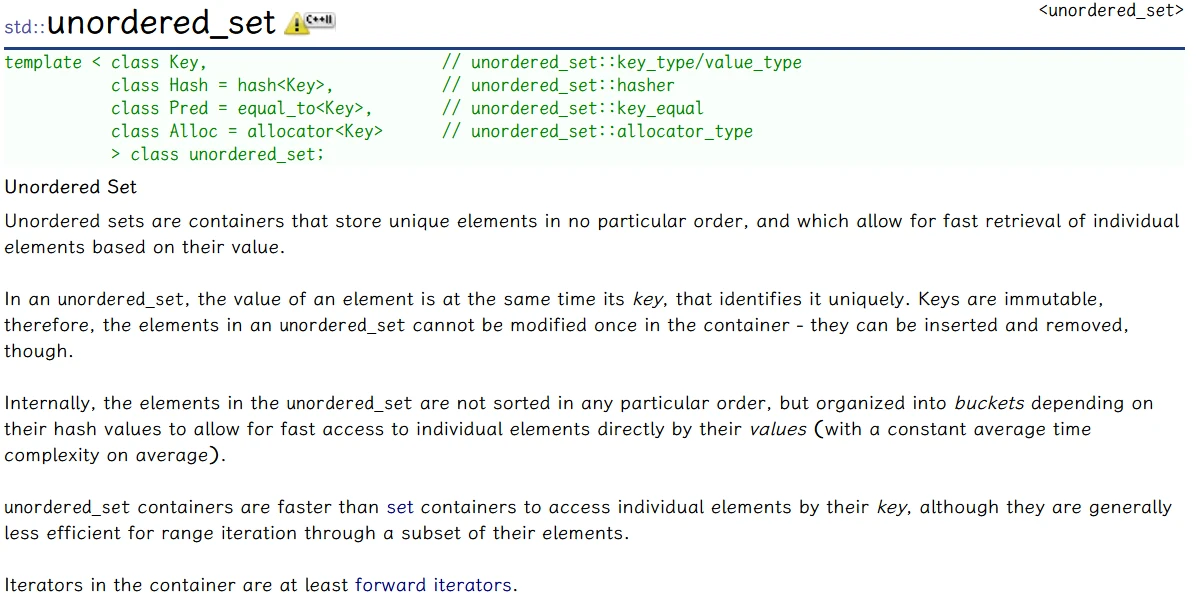
unordered_set 的介绍可以参考 unordered_map
哈希表哈希表
每个数据 与 数据的存储位置是没有关系的不通过对比, 知道元素就知道元素的存储位置, 实现出来的效果 也就类似人 看到一行不同数字, 告诉你一个数字, 你可以一眼看出这个数字在这一行中的位置哈希表 可以实现类似、接近这样的功能哈希表 存储数据 将 数据的值 和 存储位置 建立了联系, 即 可以通过数据的值 直接获取到数据的大致位置- 插入元素: 根据元素的值, 通过一定的方法 计算出此元素应该存储的位置, 然后进行存储
- 访问元素: 根据元素的值, 通过相同的方法 计算出此元素的存储位置, 然后直接访问
哈希方法 也叫散列方法, 过程中使用的转换函数 被称为 哈希函数通过 哈希方法 存储数据构造出来的结构就被称为 哈希表哈希函数
哈希函数是怎样定义的 呢?随机访问(直接给定位置进行访问数据就是一种随机访问)通过 数据的值 计算出数据在数组中需要存储的位置hash(key) = key % capacity, 函数的结果就是数据需要存储的位置key 是数据的关键值, capacity 是底层数组的容量大小
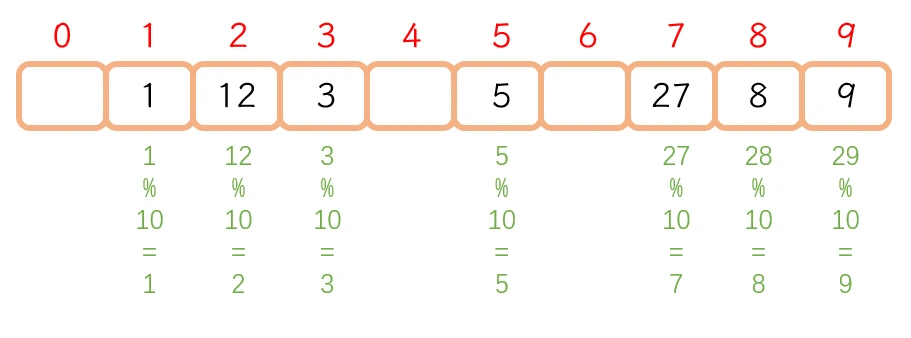
例: 给一串数据: 1 5 8 3 9 12 27
使用哈希方法 将这届数据 放入容量大小为10的数组中, 则 使用
hash(key) = key % capacity计算位置:
哈希冲突
哈希冲突 或 哈希碰撞不同关键字通过相同哈希函数计算出相同的哈希地址, 该种现象称为哈希冲突或哈希碰撞为什么会出现哈希冲突?
首先要知道,
哈希冲突是无法完全避免的, 只能尽量减少哈希冲突的出现, 但是如果哈希冲突频繁, 那么就需要考虑一下哈希函数指定是否合理了
哈希冲突的解决方法
这里的解决方法
不是为了避免哈希冲突, 而是为了解决出现哈希冲突之后数据该如何存储的问题
闭散列
闭散列, 也被称为开放定址法, 此方法 是: 出现哈希冲突时, 如果哈希表未被装满, 那么就从冲突位置 向后找空位置 将 冲突的数据存储到空位置中线性探测 或 二次探测线性探测
线性探测提供的向后找空位置的方法是: 从冲突位置向后依次找每个位置是否为空, 直到找到空位则将数据存储到此位置hash(key)%capacity + i (i = 0,1,2,3……)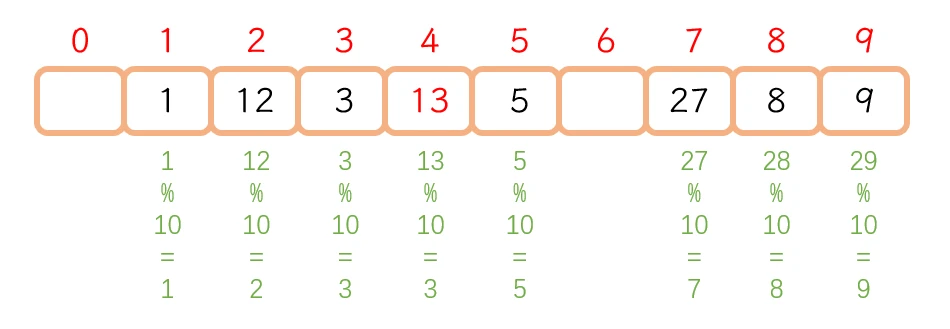
13 直接存储在 3 的后面
使用线性探测可以
非常简单的解决哈希冲突的情况, 但是弊端非常大, 此例子就可以显示出来:
会造成数据拥堵, 堆积, 有可能占据了下一个原本不会发生哈希冲突的数据的位置
且 如果堆积严重 会导致插入数据向后探测次数变多, 导致效率降低虽然 线性探测的弊端非常的大, 但是 也是结局哈希冲突的一种方法
二次探测
hash(key) % capacity + i^2 (i = 0,1,2,3……)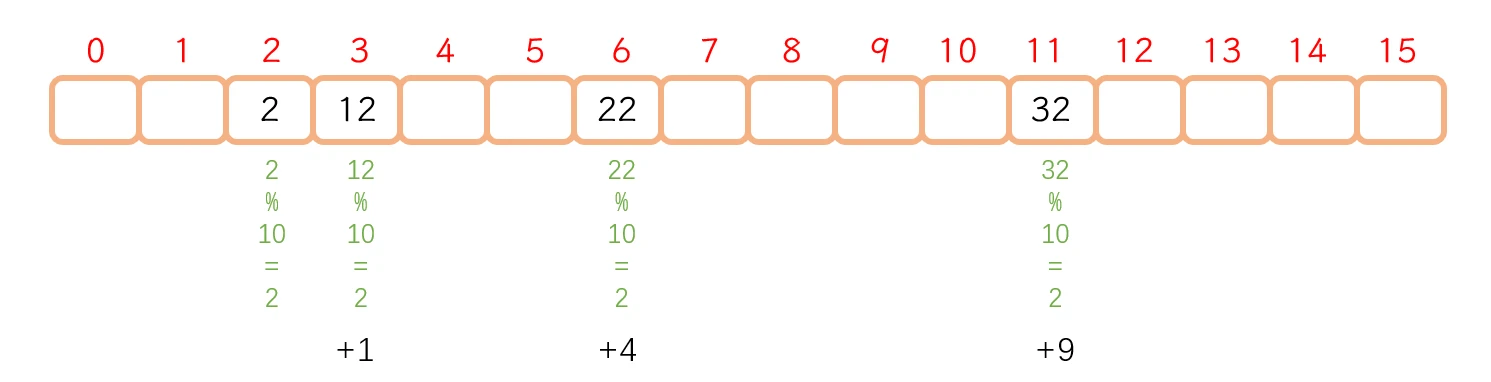
使用二次探测, 不会造成向后数据堆积的情况, 但是会造成
空间浪费太多
闭散列 数据删除
不能随意删除 的, 否则的话会影响查找哈希表查找数据时, 一般查找到空才会停止, 如果是发生了哈希冲突的数据, 则会按照处理方法向后寻找. 如果 直接删除某个发生了冲突的数据: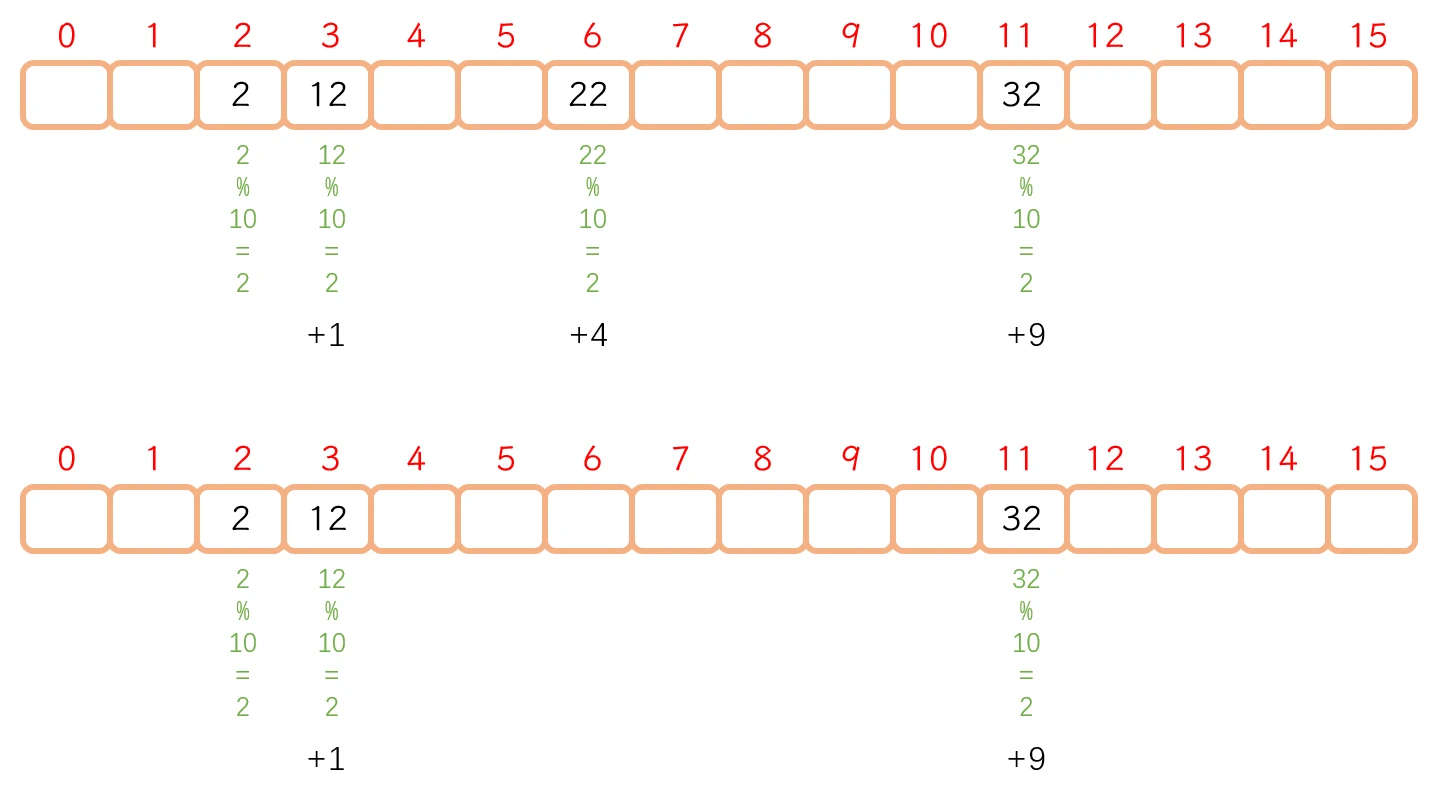
没有删除的时候, 查找 32, 则会先找到 2, 再找到 12, 再找到 22, 最后找到 32
直接删除了之后, 就会查找不到 32, 即使 32实际是在表中
因为 这是的查找流程就是: 先找到 2, 再找到 12, 再找到
第6个位置 发现为空, 停止查找
不能直接删除数据DELETE(删除), EXIST(存在), EMPTY(空)- 插入数据, 就将数据的状态改为 EXIST 表示存在
- 删除数据, 就将数据的状态改为 DELETE 表示删除
- 当前位置为空, 那么当前位置数据状态就为 EMPTY 表示空
查找访问数据, 通过数据的状态进行对比, 只有遇到 EMPTY状态时, 查找才停止, 遇到 DELETE 不停止闭散列 扩容
什么时候扩容
以 线性探测为例:
线性探测不会跳跃性的进行探测位置, 所以可以在 数组完全满了之后再进行扩容
但是 其实当数组内存储的数据 占 总容量的比例越大, 发生哈希冲突的概率就会越大, 所以 最好不要 在数组完全存储满了之后再进行扩容
一般 设置为
70%, 这个值一般被称为负载因子
而 二次探测:
二次探测 探测位置是跳跃性的, 所以 可能出现
即使数组还有空间, 计算出的哈希位置却不再数组空间范围内的情况, 此时就需要扩容了所以 二次探测 不能等到数组完全存满之后在进行扩容, 实验表明 二次探测的负载因子在50%, 即 存储的数据数量 少于 空间总容量的一半, 就可以保证 新的数据一定可以插入表中
所以 二次探测 哈希表的负载因子 一般设置为 50% 以下
怎么扩容
数据的值和数组的容量 来进行计算相对应的哈希位置的表中原来的数据 也应该与 数组新的容量进行计算 获得新的映射, 这样才能保证 查找数据正常闭散列哈希表 插入 查找 删除 模拟实现
// 枚举变量 表示状态
enum State {
EMPTY,
EXIST,
DELETE
};
// 哈希表数据类型
template<class K, class V>
struct HashData {
pair<K, V> _data;
State _state = EMPTY;
};
template<class K, class V>
class HashTable {
public:
typedef HashData<K, V> Data;
bool insert(const pair<K, V>& kv) {
if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7) { // 当 哈希表总容量为0, 或 哈希表内存储的数据个数已经达到了总容量的70% 进行扩容
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2; // 新容量为10 或 原来的 2倍
// 哈希表扩容并不是 仅仅在原来的基础上改变容量那么简单, 而是需要以新的容量作为 capacity, 对哈希表内的数据进行重新映射
HashTable<K, V> newHashTable;
newHashTable._tables.resize(newSize); // 调用vector的resize接口将新哈希表的容量改为newSize
// 遍历原来的哈希表, 将原来的哈希表内的数据映射到 新的哈希表中
for (auto& e : _tables) {
if (e._state == EXIST) { // 将 原哈希表中存在的数据 映射到新哈希表中
newHashTable.insert(e._data);
}
}
// 遍历重新映射完成之后, 将 两个哈希表的_tables 进行交换
// 就可以将当前的哈希表扩容为新的哈希表
_tables.swap(newHashTable._tables);
}
size_t startI = kv.first % _tables.size(); // 开始探测的位置
size_t hashI = startI;
size_t i = 1;
while (_tables[hashI]._state == EXIST) { // 发生哈希冲突就继续向后探测
hashI = startI + i;
i++;
hashI %= _tables.size(); // 更新需要探测的位置
}
// 探测到空位置之后
_tables[hashI]._data = kv;
_tables[hashI]._state = EXIST;
_n++;
return true;
}
Data* find(const K& key) {
if (_tables.size() == 0) {
return nullptr; // 哈希表为空 查找失败
}
size_t startI = key % _tables.size();
size_t hashI = startI;
size_t i = 1;
while (_tables[hashI]._state != EMPTY) { // 当 当前探测位置不为空时, 进入循环 继续查找
if (_tables[hashI]._state != DELETE && _tables[hashI]._data.first == key) {
// 当 当前探测位置数据没有被删除 且 与查找数据相等时 就返回当前位置地址
return &_table[hashI];
}
// 当前位置的数据 不是 查找的数据 就更新探测位置 继续查找
hashI = startI + i;
i++;
hashI %= _tables.size();
}
return nullptr; // 走出循环 就表示没有找到
}
bool erase(const K& key) {
Data* ret = find(key);
if (Data) {
ret->_state = DELETE;
_n--;
return true;
}
else {
return false;
}
}
private:
vector<Data> _tables;
size_t _n = 0;
};开散列, 开散列比闭散列更加具有优势开散列
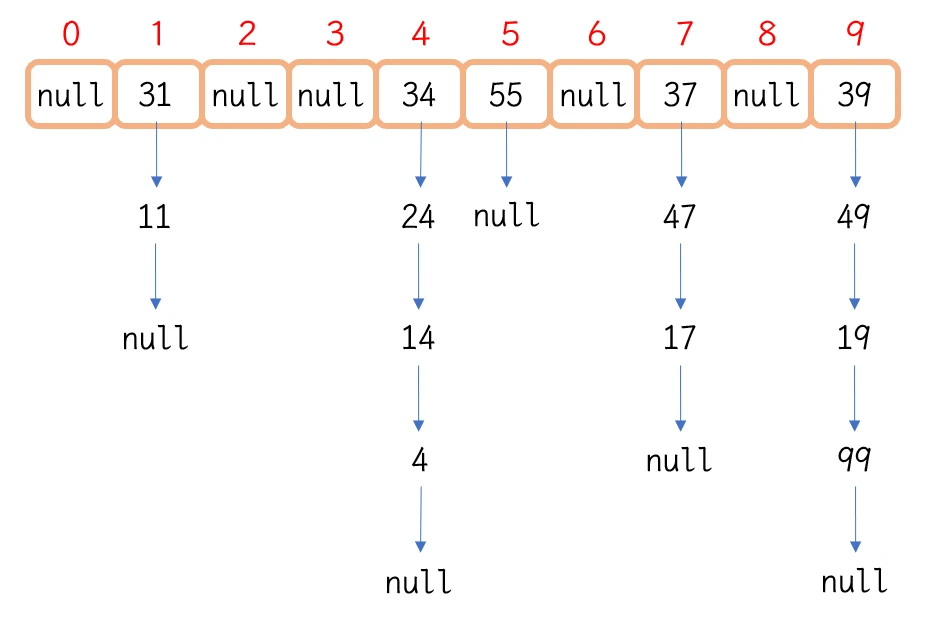
链地址法\开链法, 构建方法 依旧是通过哈希函数计算哈希地址, 但是 开散列中, 哈希地址相同的数据(即发生哈希碰撞的数据) 归为一个集合, 此集合以单链表的形式存在, 被称为桶, 各个链表的头节点被存放在哈希表中, 所以此种结构也被称为哈希桶 (以下均称为哈希桶)将
4 11 99 17 14 24 47 19 31 49 37 39 34 55以此插入 哈希桶中, 哈希桶的结构就可以示意为:将 哈希地址相同的数据 以
单链表的形式存储在各个位置中
闭散列堆积数据会导致占用其他数据位置 的问题, 因为 发生哈希冲突的数据都被存储在了一个链表中 不会对其他链造成影响哈希桶的扩容
扩容什么时候扩容?
什么时候扩容?哈希桶的扩容可以提供两个方向的想法:
当 存储的数据节点 与 数组的容量 存在一定的关系时, 进行扩容, 这个关系合理就可以, 比如 相同时
当 桶长度达到某个值时, 进行扩容
此方法, 需要在哈希表的结构中 添加一个存储桶的最长长度的变量
注意
频繁扩容同样非常影响哈希桶的效率, 谨慎选择
怎么扩容?
弊端过大 :-
哈希桶中数组存储的内容是链表, 如果遍历链表数据 并插入到新的哈希桶中, 需要经过一些过程: 创建新的临时表->多次创建新节点 并插入到新表中->交换数组->释放临时表
在此过程中, 存在一个开销非常大的操作 即 释放临时表, 因为哈希桶的数组中存储的是链表 即使 临时表的数组与原表的数组进行了交换, 但是数据量是没有改变的, 临时对象的释放过程是需要对数组中存储的单链表进行遍历并释放节点的 这个开销已经至少是
O(N)了, 这个开销非常大
将 原数组中的节点 转移映射到 新的数组中, 再将 新数组作为 哈希桶的底层数组, 就可以避免 创建节点 和 释放链表的过程不需要创建节点 是因为 直接将原节点 转移到了 新的数组中
不释放链表, 是因为
原数组中的节点已经被映射转移到新数组中了, 并且 新数组作为了哈希桶的底层数组, 所以 另一个数组已经空了, 只需要释放一个空的数组就可以了
哈希桶 插入 查找 删除 模拟实现
// 数据节点 结构
template<class K, class V>
struct HashNode {
pair<K, V> _data;
HashNode<K, V>* _next;
HashNode(const pair<K, V>& kv)
:_data(kv)
,_next(nullptr)
{}
};
template<class K, class V>
class HashTable {
typedef HashNode<K, V> Node;
public:
// 由于 数组内存储的链表是自定义的, 所以需要定义析构函数将链表释放
~HashTable() {
// 遍历哈希桶 释放节点
for (int i = 0; i < _tables.size(); i++) {
Node* cur = _tables[i];
while (cur) {
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}
bool insert(const pair<K, V>& kv) {
if (find(kv.first)) {
return false; // 设计 不可重复存储数据
}
// 设置 当负载因子== 1时 扩容
/*if (_tables.size() == _n) {
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
// 这种方法 非常的影响效率
// 因为这种方法 调用了 insert接口, 在开散列的处理中使用insert接口 会创建新的节点, 开销过大
// 并且, 由于创建了新的 哈希桶, 所以在 下面循环结束的时候 新的临时的哈希桶会被释放 释放需要遍历哈希桶 又是影响效率
HashTable<K, V> newHashTable;
newHashTable._tables.resize(newSize, nullptr);
// 遍历原哈希桶 在新哈希桶中重新映射
for (int i = 0; i < _tables.size(); i++) {
Node* cur = _tables[i];
while (cur) {
newHashTable.insert(cur->_data); // 新哈希桶中插入 当前节点的存储数据
cur = cur->_next;
}
}
_tables.swap(newHashTable._tables);
}*/
// 上面的扩容方法 非常的影响效率且开销过大
// 下面的另一种方法, 不调用insert, 不创建新的哈希桶 不创建新的节点 也不需要释放新的空间
// 而是 直接将 旧数组中的节点 重新计算映射到新的数组中, 再将 哈希桶的数组更新为新数组就可以了
if (_tables.size() == n) {
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*> newTable;
newTable.resize(newSize, nullptr);
for (int i = 0; i < _tables.size(); i++) {
Node* cur = _tables[i];
while (cur) {
Node* next = cur->_next; // 后面会 使cur->_next 变成 数组中存储的头节点, 所以 下一个节点提前记录
size_t hashI = cur->_data.first % newTable.size(); // 以新数组的容量计算 对应的哈希地址
cur->_next = newTable[hashI]; // 插入的节点 与 newTable存储的头节点相连接
newTable[hashI] = cur;
cur = next; // 更新 cur
}
_tables[i] = nullptr; // 原数组的内容已被转移到新数组中 将原数组的内容置空
}
_tables.swap(newTable);
}
// 扩容完毕, 下面插入数据
size_t hashI = kv.first % _tables.size();
// 找到该向数组中第几个位置插入数据
// 然后进行头插
Node* newNode = new Node(kv); // 以kv数据创建新的节点
newNode->_next = _tables[hashI]; // 将数组中存储的链表的头节点连接在新节点之后
_tables[hashI] = newNode; // 新节点存储到数组中
_n++;
return true;
}
Node* find(const K& key) {
if (_tables.size() == 0) {
return nullptr;
}
size_t hashI = key % _tables.size();
Node* cur = _tables[hashI];
while (cur) {
if (cur->_data.first == key) {
return cur; // 找到返回节点
}
cur = cur->_next;
}
return nullptr;
}
bool erase(const K& key) {
/*
// 一般思路
size_t hashI = key % _tables.size();
Node* cur = _tables[hashI];
Node* prev = nullptr;
while (cur) {
if (cur->_data.first == key) {
if (cur == _tables[hashI]) {
// 需要删除的节点是 数组中存储链表的头节点
_tables[hashI] = cur->_next;
}
else {
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}*/
// 特殊思路, 禁止获取 prev 以及 使用next的数据作为判断条件
// 采用数据替换:
// 要删除 cur节点的数据, 就将cur的数据 用 cur->next的数据 覆盖掉, 再将 cur与 cur->next->next 建立连接之后 释放cur->next节点
// 这只是一种思路, 并不是说这种方法更好, 事实上这种方法并没有上面哪一种方法好, 因为 这种方法 一定会产生数据的拷贝
// 当数据内容过大 过多时, 开销过大
size_t hashI = key % _tables.size();
Node* cur = _tables[hashI];
while (cur) {
if (cur->_data.first == key) {
if (cur->_next == nullptr) {
// 如果当前节点是单链表中的最后一个节点时
// 是没有下一个结点的, 所以不能与下一个节点进行数据的替代
// 但是可以与 头节点进行数据的替代, 然后头删
Node* head = _tables[hashI];
cur->_data = head->_data;
_tables[hashI] = head->_next;
delete head;
head = nullptr;
}
else {
cur->_data = cur->_next->_data;
cur->_next = cur->_next->_next;
delete cur->_next;
}
_n--;
return true;
}
cur = cur->_next;
}
return false;
}
private:
vector<Node*> _tables;
size_t _n = 0; // 记录数组存储数据的数量
};string 的哈希值
不能直接进行 求余计算 的对象, 该如何使用哈希函数计算对应的哈希地址呢?当然可以使用 字符串的长度 或者 首字符的ASCII码值 来进行计算, 但是这样的话 会频繁发生太多的哈希冲突:
- 字符串长度:
abcd和cdef就会发生哈希冲突- 首字符的ASCII码值:
aijsfjioasjdioajfijixnvccxov和a就会发生哈希冲突也可以用 字符串所有字符的ASCII码和来进行计算, 但是 这样也没有什么太大的优化, 因为还是不能明显区分 :
abcddcba等
size_t BKDRHash(const string& str) {
size_t hash = 0;
for(auto c : str) {
hash = hash * 131 + c; // 也可以乘以31、131、1313、13131、131313..
}
return hash;
}大家可以测试一下, 通过此算法计算出的 string的哈希值, 发生冲突的概率非常小
仿函数 解决不同类型 哈希值的计算
仿函数 就又需要上场了
第三个 Hash , 需要传入的函数就是 取key类型的哈希值的仿函数
template<class Key>
struct defaultHashFcn { // 默认的仿函数, 处理可以直接转换成 size_t的类型
size_t operator()(const Key& k) {
return (size_t)k;
}
};
// 针对string类型的仿函数
template<class Key>
struct stringHashFcn {
size_t operator()(const Key& str) {
size_t hash = 0;
for (auto c : str) {
hash = hash * 131 + c;
}
return hash;
}
};// 缺省值给默认的仿函数
template<class K, class V, class HashFcn = defaultHashFcn<K>>
class HashTable {};size_t hashI = cur->_data.first % _tables.size();
↓
HashFcn hf;
size_t hashI = hf(cur->_data.first) % _tables.size();
size_t hashI = key % _tables.size();
↓
HashFcn hf;
size_t hashI = hf(key) % _tables.size();
size_t hashI = kv.first % _tables.size();
↓
HashFcn hf;
size_t hashI = hf(kv.first) % _tables.size();注意 仿函数的使用,
需要实例化仿函数对象 然后通过对象使用仿函数
将 针对string类型计算哈希值的仿函数, 改成默认仿函数的特化形式第三个模板参数的传入默认仿函数的缺省值 就可以直接处理string类型template<class Key>
struct defaultHashFcn { // 默认的仿函数, 处理可以直接转换成 size_t的类型
size_t operator()(const Key& k) {
return (size_t)k;
}
};
template<>
struct defaultHashFcn<string> { // 默认仿函数 针对string类型的特化
size_t operator()(const string& str) {
size_t hash = 0;
for (auto c : str) {
hash = hash * 131 + c;
}
return hash;
}
};使用仿函数的 插入 查找 删除 模拟实现 相关代码
template<class Key>
struct defaultHashFcn { // 默认的仿函数, 处理可以直接转换成 size_t的类型
size_t operator()(const Key& k) {
return (size_t)k;
}
};
template<>
struct defaultHashFcn<string> { // 默认仿函数 针对string类型的特化
size_t operator()(const string& str) {
size_t hash = 0;
for (auto c : str) {
hash = hash * 131 + c;
}
return hash;
}
};
// 针对 string的仿函数的非特化版
/*template<class Key>
struct stringHashFcn {
size_t operator()(const Key& str) {
size_t hash = 0;
for (auto c : str) {
hash = hash * 131 + c;
}
return hash;
}
};*/
// 数据节点 结构
template<class K, class V>
struct HashNode {
pair<K, V> _data;
HashNode<K, V>* _next;
HashNode(const pair<K, V>& kv)
:_data(kv)
,_next(nullptr)
{}
};
template<class K, class V, class HashFcn = defaultHashFcn<K>>
class HashTable {
typedef HashNode<K, V> Node;
public:
// 由于 数组内存储的链表是自定义的, 所以需要定义析构函数将链表释放
~HashTable() {
// 遍历哈希桶 释放节点
for (int i = 0; i < _tables.size(); i++) {
Node* cur = _tables[i];
while (cur) {
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}
bool insert(const pair<K, V>& kv) {
if (find(kv.first)) {
return false; // 设计 不可重复存储数据
}
HashFcn hf;
if (_tables.size() == _n) {
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*> newTable;
newTable.resize(newSize, nullptr);
for (int i = 0; i < _tables.size(); i++) {
Node* cur = _tables[i];
while (cur) {
Node* next = cur->_next; // 后面会 使cur->_next 变成 数组中存储的头节点, 所以 下一个节点提前记录
size_t hashI = hf(cur->_data.first) % newTable.size(); // 以新数组的容量计算 对应的哈希地址
cur->_next = newTable[hashI]; // 插入的节点 与 newTable存储的头节点相连接
newTable[hashI] = cur;
cur = next; // 更新 cur
}
_tables[i] = nullptr; // 原数组的内容已被转移到新数组中 将原数组的内容置空
}
_tables.swap(newTable);
}
// 扩容完毕, 下面插入数据
size_t hashI = hf(kv.first) % _tables.size();
// 找到该向数组中第几个位置插入数据
// 然后进行头插
Node* newNode = new Node(kv); // 以kv数据创建新的节点
newNode->_next = _tables[hashI]; // 将数组中存储的链表的头节点连接在新节点之后
_tables[hashI] = newNode; // 新节点存储到数组中
_n++;
return true;
}
Node* find(const K& key) {
if (_tables.size() == 0) {
return nullptr;
}
HashFcn hf;
size_t hashI = hf(key) % _tables.size();
Node* cur = _tables[hashI];
while (cur) {
if (cur->_data.first == key) {
return cur; // 找到返回节点
}
cur = cur->_next;
}
return nullptr;
}
bool erase(const K& key) {
HashFcn hf;
size_t hashI = hf(key) % _tables.size();
Node* cur = _tables[hashI];
Node* prev = nullptr;
while (cur) {
if (cur->_data.first == key) {
if (cur == _tables[hashI]) {
// 需要删除的节点是 数组中存储链表的头节点
_tables[hashI] = cur->_next;
}
else {
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
private:
vector<Node*> _tables;
size_t _n = 0; // 记录数组存储数据的数量
};作者: 哈米d1ch 发表日期:2022 年 11 月 11 日