算法 2023 年 2 月 20 日

[C++] 位图与布隆过滤器的相关介绍

哈希是一种思想, 位图和布隆过滤器是哈希思想的实现的一种

哈希是一种思想, 除了之前文章中介绍的一些使用哈希思想实现的哈希表之外, 哈希思想的应用还有其他的方面。也就是本篇文章所介绍的位图和布隆过滤器

位图

在正式介绍位图之前，先分析一道题：

给40亿个不重复的无符号整数，没排过序。如何快速判断一个数是否在这40亿个数中？

首先分析问题：

40亿个无符号整数, 1个无符号整数4字节, 40亿个就是160亿字节

如果将这40亿个整数存放到内存中, 则需要 16GB 的内存

所以为了解决这类问题将所有数据存储到内存中, 不太现实

题目要求要快速判断, 所以遍历的方法首先就可以被OUT

那么可以想到的比较快速的查找方法就是：二分查找

但是二分查找的前提条件是：1. 数据必须有序 2. 数据必须存储在连续的内存中

第一个条件可以用外排序解决, 但是第二个问题一般是没有办法解决的, 因为没有办法保证如此多的内存都是连续的

而位图就可以不浪费空间的解决这样的问题

什么是位图

一般来说解决一个数是否在一堆数的问题需要在一堆数中进行查找。但是以亿为计量单位的数据不太适合直接对数据进行查找, 所以想要快速的判断出海量数据中是否存在某个数, 就需要另外的方法, 位图就是一种方法

数据是否在海量数据中存在，只有两种状态：存在或不存在。这两种状态刚好可以用一个比特位来表示, 因为一个比特位上可以出现的数据只有 1和0, 可以用来表示存在或不存在。

而位图, 就是用比特位来存放某种状态的结构, 适用于海量数据, 数据无重复的场景。通常判断数据是否存在

位图实现的思想使用的是哈希的思想, 将表示数据是否存在的状态映射到比特位上, 不同的数据映射到不同的比特位

位图的实现

位图的结构

位图的原理是用比特位表示数据的存在与不存在两种状态，那么最简单最方便控制的方式就是使用 vector<char> 作为位图实现的底层, 那么每一个vector单元就是8个比特位(如果用int, 则每个单元就是32个比特位)

class bitset {
private:
	vector<char> _bit;
}

位图的构造函数

实例化位图对象是需要确定开辟的比特位的个数的, 所以位图的构造函数就应该实现这样的功能。

以char来作为vector的单元类型, 那么如果需要8个比特位的话就至少需要开辟1个单元; 如果需要14个比特位的话, 就至少需要开辟2个单元; 如果需要16个比特位的话, 也至少需要开辟2个单元。

那么构造函数的实现：

class bitset {
pubilc:
	bitset(size_t N) {
		_bit.resize(N/8 + 1, 0);	// 需要开辟N/8+1个空间, +1是为了保证比特位足够, 最多也就浪费8个比特位
	}

private:
	vector<char> _bit;
}

数据在位图中的映射

位图思想是哈希的思想, 所以每个数据是需要唯一映射在比特位上的

以 14 这个数为例, 在位图中映射的位置就应该是第2个单元的第2位上(右–>左 0–>7)

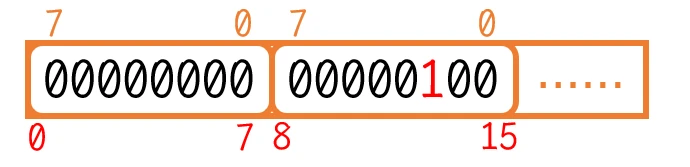
以此规则, 添加可以将数据映射的比特位设置为 0 或 1 的接口：

set：

void set(size_t x) {
	size_t i = x / 8;		// 算出x映射在第i个单元
	size_t j = x % 8;		// 算出x映射在第i个单元的第j个比特位上
	
	_bit[i] |= (1 << j);	// 将指定比特位设置为1
}

reset：

void reset(size_t x) {
	size_t i = x / 8;
	size_t j = x % 8;
	
	_bit[i] &= (~(1 << j));		// 将指定比特位设置为0
}

判断数据是否在位图中

在所有数据映射到位图中之后, 映射到的比特位都已经变成了1, 这样再判断某个数据是否在某些数据中时, 就可以直接判断此数据在位图中所映射的位置是否为1。如果为1, 则在; 否则, 不在。

test：

bool test(size_t x) {
	size_t i = x / 8;
	size_t j = x % 8;
	
	return _bit[i] & (1 << j);
	// 只要将整个单元数据 与上 只有第j位为1的数, 那么就可以根据结果判断出此位是否为1, 进而判断出数据是否在位图中
}

位图解决问题

既然一个比特位可以表示一个数据是否存在, 那么40亿个数据需要多少个比特位来表示呢？

许多人的第一感觉应该是 40亿个，但其实不是。应该是 INT_MAX个而不是 40亿。为什么？因为比特位表示的是整数是否存在, 所以比特位的个数需要能够表示所有整数的存在状态, 而不是给定数据的个数。而 int 的范围就是INT_MAX, 所以需要INT_MAX个比特位才能够表示所有整数的存在状态

也就是说, 即使是1000个亿的整型数据, 也是需要INT_MAX个比特位; 不过, 如果知道数据的范围的话, 就只需要范围内个数的比特位就可以了

所以使用位图解决问题首先需要创建一个足够包含所有数据映射位置的位图, 然后对已有数据进行映射和判断, 就可以解决问题

当然, 位图的首次映射也可能是一个漫长的遍历过程, 但是只要位图构建完成, 今后的数据判断的时间复杂度都将只是O(1)

构建INT_MAX位的位图, 至少需要使用256M-1bit=2^31-1bit

总结

位图的原理是使用哈希思想将整型数据的某种状态映射到对映比特位上, 进而方便查找数据的某种状态

因为其不直接存储数据内容的特点, 位图有着节省空间的优点, 再加上哈希思想的运用其查找数据状态速度也非常的快

但是很明显, 因为位图每个比特位最多只能表示两种状态, 要想准确的存储数据状态, 就只能处理整型数据, 其他数据都会发生哈希冲突

布隆过滤器

上面介绍的位图, 可以简单的处理海量整型数据。而对非整型的数据(浮点数、字符串等), 无法使用位图进行较为准确的处理, 比如：

当某个文件中存储有100亿个ip地址(可能相同)时, 怎么能将这些ip地址准确的映射到位图中呢？

答案显然是不可能的, 因为ip地址很明显是属于字符串数据的, 字符串的数据想要映射到位图中, 就先要将字符串数据通过哈希算法计算为整型数据, 然后再将对应的整型数据映射到位图中

而使用哈希算法将字符串转换为整型, 一定会发生哈希冲突, 这是无法避免的。那么既然会发生哈希冲突, 位图就会变得非常不准确

而为了减少哈希冲突, 提高准确率, 所以对类似的数据会使用多个哈希算法算出多个哈希值分别映射到不同的比特位上, 这样的方法就被称为布隆过滤器（BloomFilter）

这样的话, 一个key数据就再位图上映射了多个位置, 只有这些位置上同时表示数据存在时, key数据才真正存在：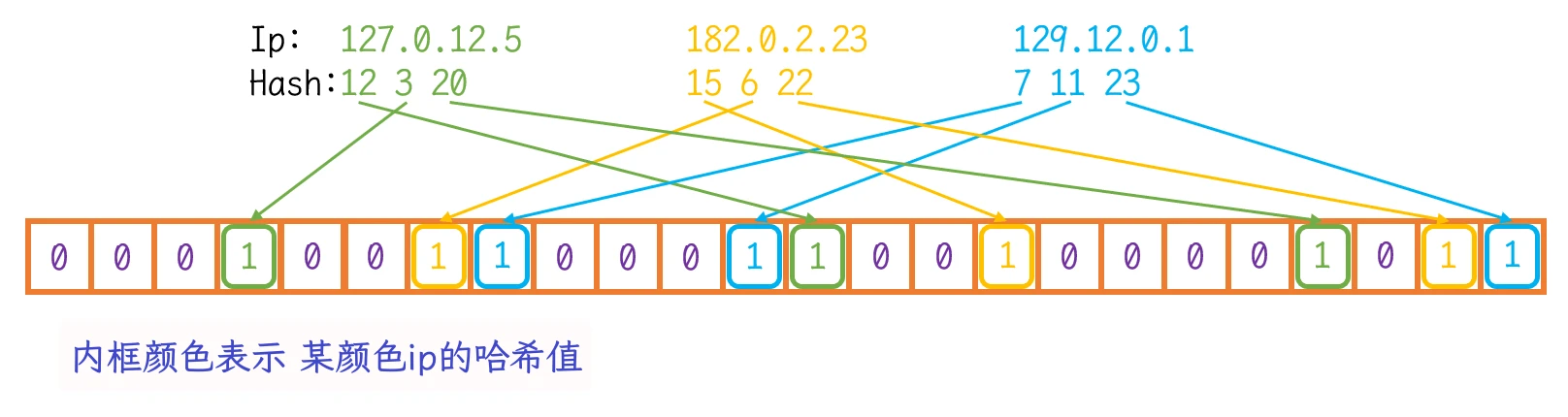

最左按第0位算

意思为：当ip计算出的三个不同的哈希值再位图中映射同时存在时, 表示此ip存在。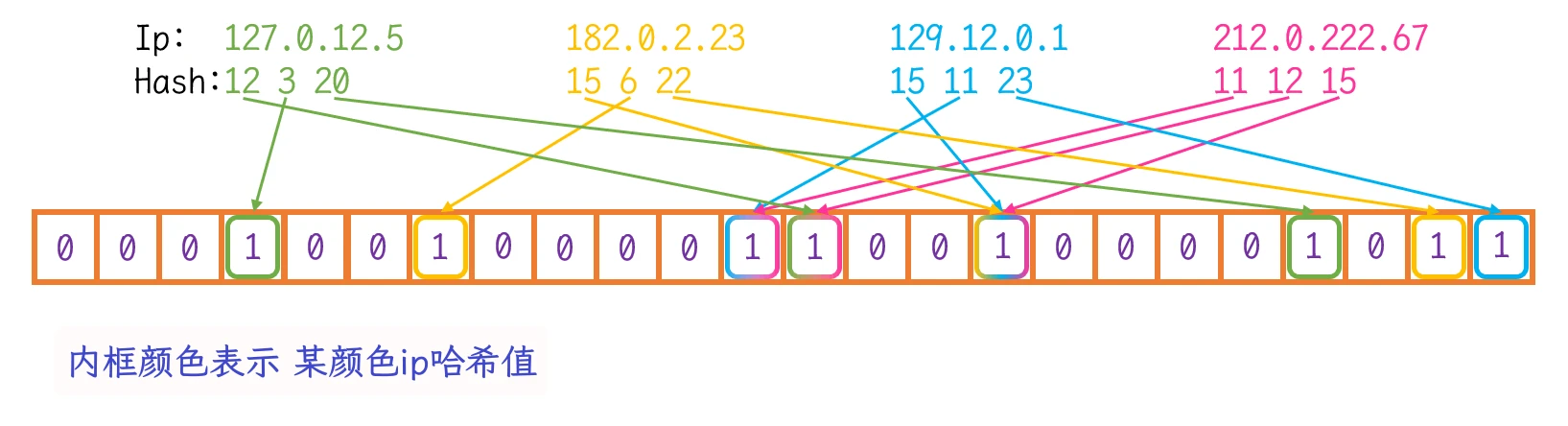

布隆过滤器其实就是针对非整型数据的位图, 布隆过滤器可以存储非整型数据的存在状态, 但是即使布隆过滤器已经针对减少哈希冲突做出了一定的方案, 也并不能完全解决哈希冲突

依旧以ip的问题为例：

在此例中, 粉色ip(212.0.222.67)计算出的三个哈希值分别是11、12、15, 而这三个哈希值也分别在其他的ip哈希值中。

也就是说同一个比特位可能被不同的原数据计算出的相同哈希值映射, 这也就可能会出现下面这种情况：

将粉色ip的映射在位图中删除：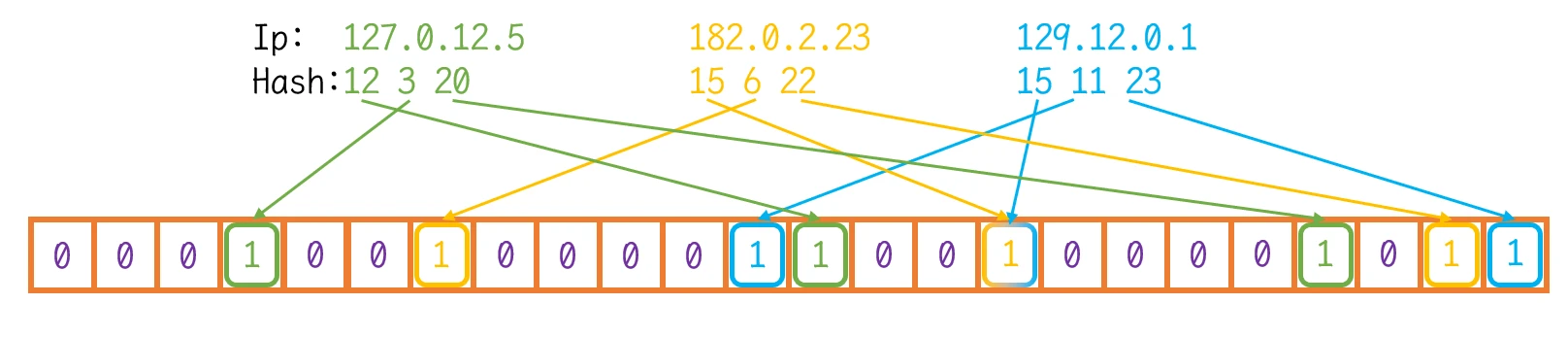

但是通过观察可以发现, 原粉色ip(212.0.222.67)计算出的三个哈希值11、12、15, 依旧映射在位图中, 这也说明了如果此时查找 ip212.0.222.67. 依旧可以在位图中查找到, 即使此ip实际并没有在位图中映射：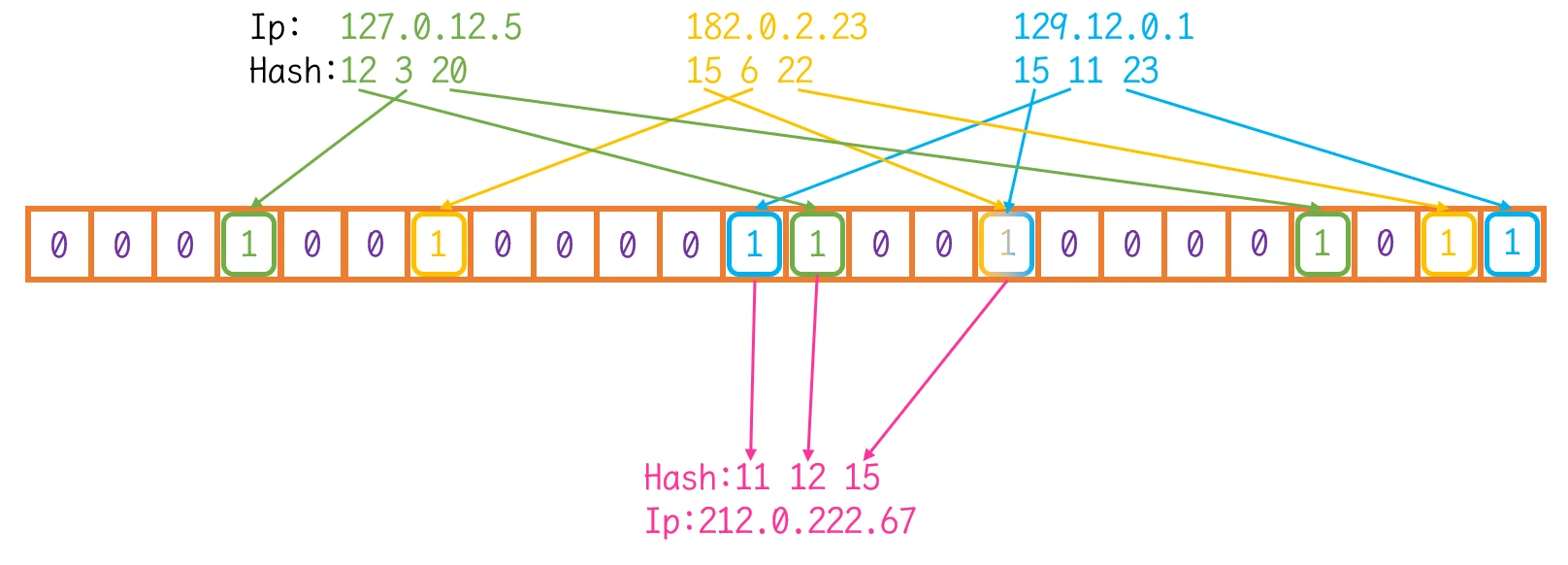

使用多个哈希值进行映射减少了发生哈希冲突的概率, 但并不能完全避免哈希冲突。存在哈希冲突就有可能在查找时发生错误或误判, 即有一定的误报率

布隆过滤器的误报率, 与哈希算法的个数、布隆过滤器比特位的个数以及需要映射的数据的个数都有关系。但具体的关系不再介绍, 这里推荐另一篇文章：

详解布隆过滤器的原理，使用场景和注意事项

此文章中间部分通过数学与图例, 分析了布隆过滤器误报率相关因素的的影响关系

那么 布隆过滤器究竟是什么？

总的来说, 布隆过滤器其实是针对处理非整型数据的位图。

由于不同的非整型数据使用哈希函数计算哈希值可能会相同, 进而在映射时会发生哈希冲突, 为了减少哈希冲突, 布隆过滤器在位图的基础上对非整型数据使用多个哈希函数计算哈希值, 再对计算出的所有哈希值在位图中进行映射。

这样一个非整型数据在位图中存在多个哈希值映射, 间接了减少了数据在位图中的冲突。

布隆过滤器的数据删除

首先想一个问题, 要为布隆过滤器实现数据删除的操作, 会存在什么问题？

删除一个数据, 需要删除多个哈希值映射
一个哈希值映射, 可能是多个数据的哈希值映射, 如果为了删除数据而直接删除此位置的哈希值映射可能会影响其他的数据

暂时只有这两个大问题, 第一个问题其实就是删除功能该如何实现的问题, 可以先放一放

那么对于第二个问题, 该如何解决一个比特位的映射, 可能是多个数据共同占用这一位这个问题呢？

在上图中展示的IP中, 如果为了删除粉色IP 进而直接删除其在比特位中的映射, 即：

将粉色IP哈希值的映射位直接删除, 那么会造成什么问题？

可以发现, 其他三个IP的哈希值在比特位中的映射都已经受到了影响。这三个IP在查找时, 已经无法查找到了：

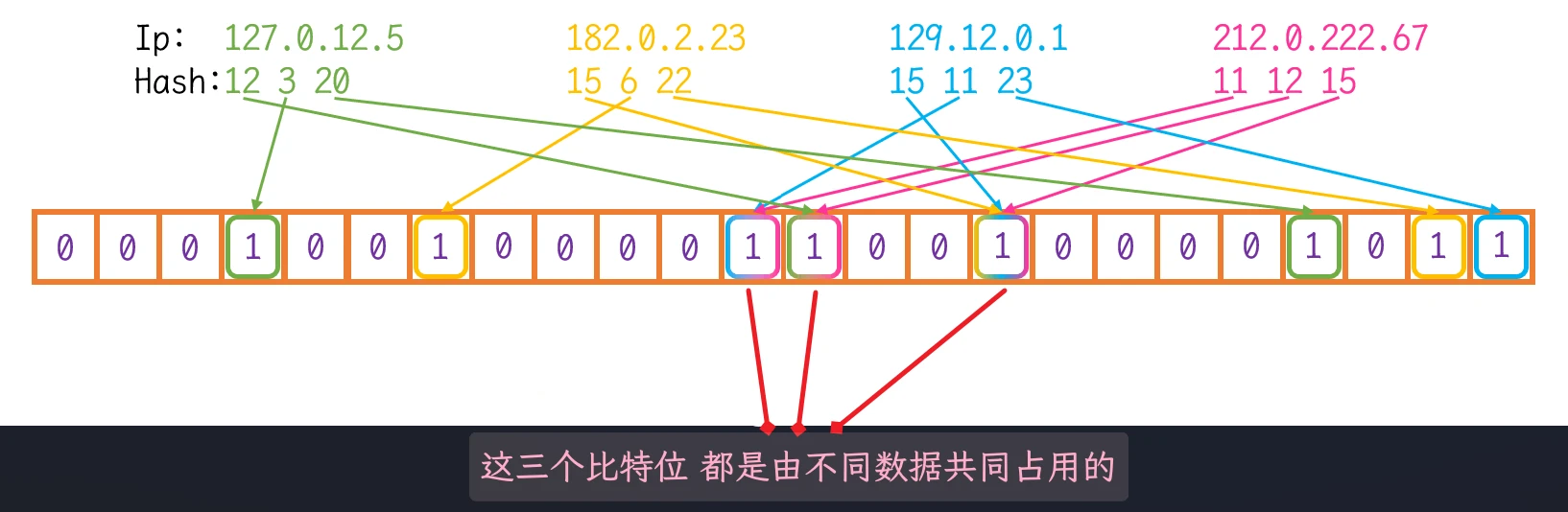
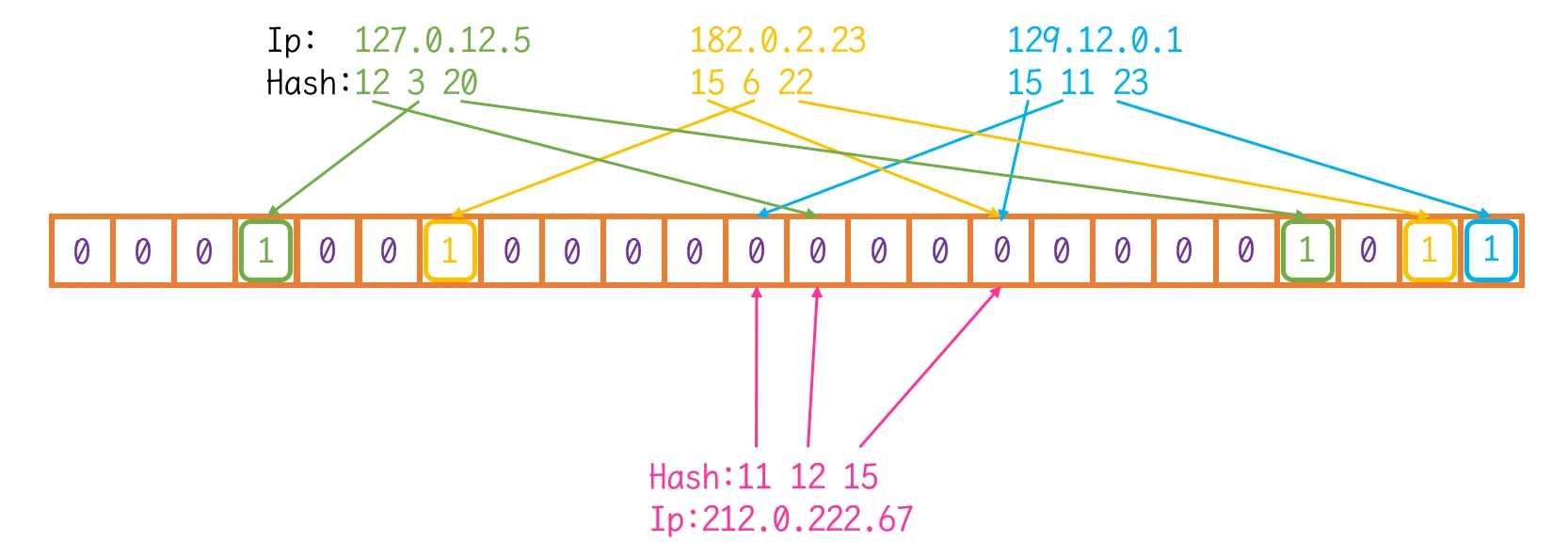
绿色IP 缺少了第12位的映射
蓝色IP 缺少了第11、15位的映射
黄色IP 缺少了第15位的映射

那么, 如何解决类似这样的问题呢？

要解决这样的问题, 只能对布隆过滤器进行改装, 对布隆过滤器的映射位添加一个计数的功能：

当此为没有被映射的时候, 此位的映射计数记0; 每有一个数据的哈希值映射到此位, 此位的映射计数+1

但是添加计数还存在一个问题：

如何进行计数？是使用其他容器然后针对各映射位进行计数？还是在布隆过滤器本身进行计数？

布隆过滤器是为了处理海量数据节省内存而设计出来的, 如果再使用其他容器, 那么节省内存这个优势就没有了。

那么就应该在布隆过滤器本身进行计数

在布隆过滤器本身进行计数, 有一个非常巧妙的实现思路：传统的布隆过滤器是每一个比特位表示一个哈希值的映射。可以通过设计, 使布隆过滤器的多个比特位表示一个哈希值的映射。当然, 这多个比特位中还是只有一个比特位表示哈希值的具体映射, 其他比特位其实是用来计数的。

这种思路的布隆过滤器被称为 Counting BloomFilter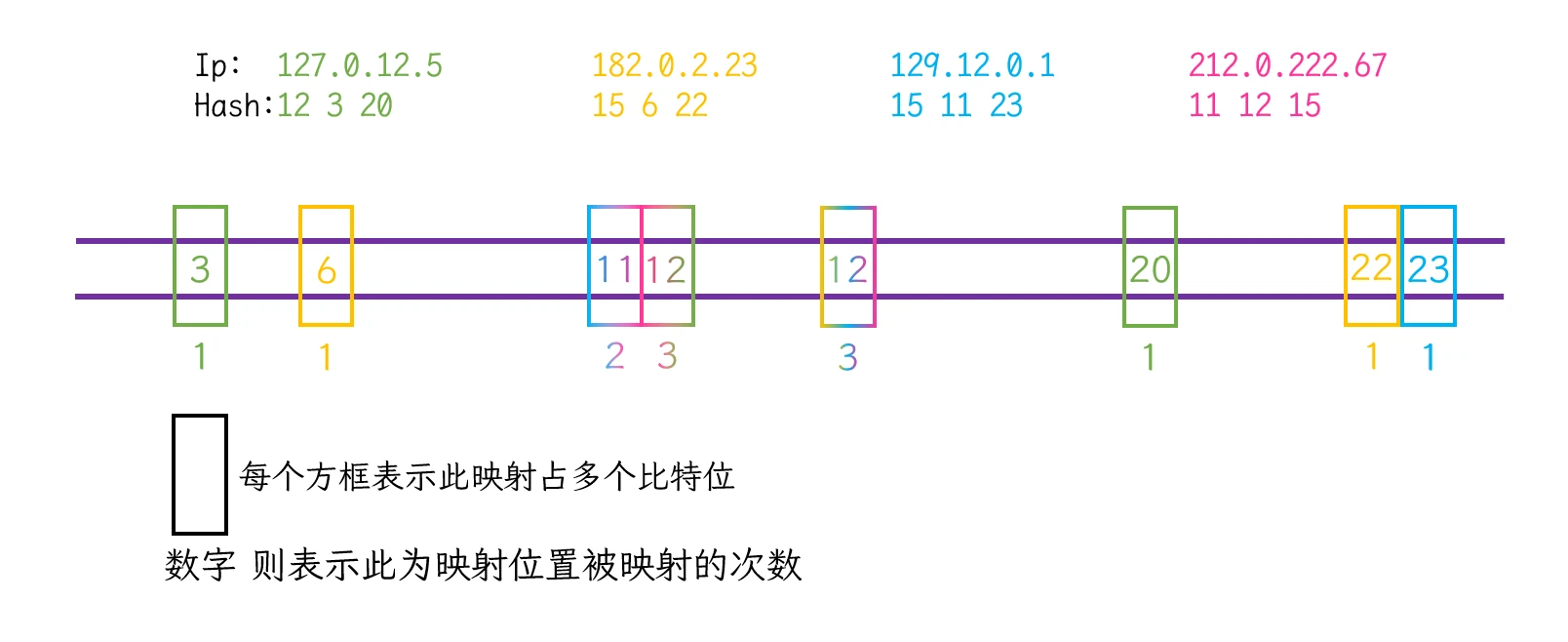

以多个比特位实际表示一个哈希映射位和映射次数的这种结构, 可以实现对原数据的删除。

以上图为例, 需要删除某个ip时, 通过哈希算法计算出对应的映射位及找到相应的映射次数, 再将映射次数-1, 就可以看作实现了对数据的删除。当映射次数减为0时, 再将这多个比特位全部置0, 表示多位无映射

比如删除蓝色和粉色ip, 之后Counting BloomFilter的大致模型就应该是：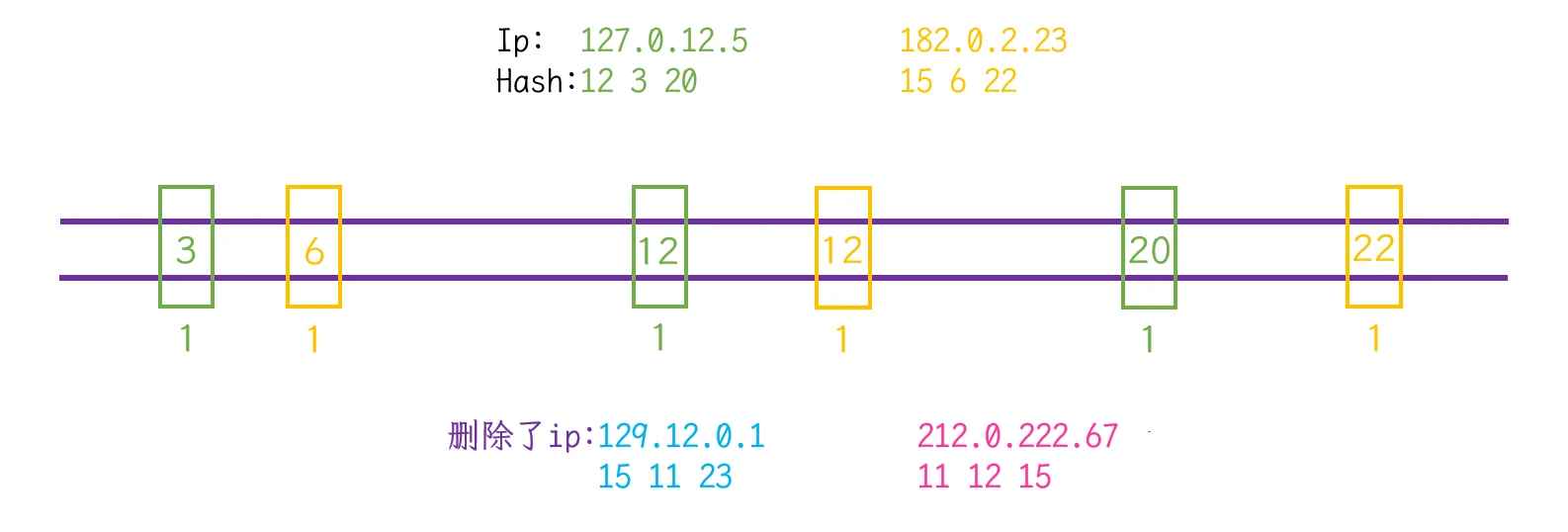

这样的思路, 就可以实现布隆过滤器对数据的删除

Counting BloomFilter的弊端

布隆过滤器的设计初衷, 是为了节省空间并处理海量非整型数据是否存在的问题。

而增添一个删除功能就会使其占用内存成倍的增加, 具体增加多少则在于实际多少个比特位映射一个哈希值

且当同一个哈希值映射次数过多时, 可能还需要增加一个哈希值需要映射的比特位

这些都会造成对资源的浪费

为什么是过滤器

前边提到过一个名词：误报率。

即布隆过滤器使用多个哈希值进行映射减少了发生哈希冲突的概率, 但并不能完全避免哈希冲突。存在哈希冲突就有可能在查找时发生错误或误判, 即有一定的误报率

也就是说, 布隆过滤器并不能像位图一样准确地映射及表示原数据的存在状态, 就会导致在布隆过滤器中查找数据的时候可能会发生错误。

虽然通过布隆过滤器查找数据存在一定的误报率, 但也并不是完全不准确的。

在布隆过滤器中查找数据的存在状态, 结果一定是两种：存在或不存在

当查找结果是不存在的时候, 可以 100%地肯定, 此数据一定没有在布隆过滤器中(或者说一定没有在原数据堆中)

但当查找结果是存在的时候, 一般是不能做出肯定的答复的, 需要进一步进行准确的判断, 比如在数据库中再次进行准确的查找。

也就是说 找不到就一定不存在, 找到了却不一定存在。这也是布隆过滤器的被称为过滤器的原因, 虽然不能准确的查找, 但是却可以过滤掉一部分数据

海量数据的处理

哈希切割

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

我们都知道, 特定的哈希算法可以给不同的数据赋予各自可能唯一的哈希值。那么当海量的数据不能一下存储到内存中进行数据分析时, 可以使用特定的哈希算法计算出数据的哈希值, 并将哈希值相同的数据存放到另一个文件中, 思路像是将海量的数据按照哈希值进行分类, 将海量数据文件分为诺干小文件。此种方法就被称为哈希切割

那么针对此题目, 就可以设计哈希算法, 分别计算100G大小文件中的IP地址的哈希值, 将哈希值相同的IP存放到同一个文件中, 然后在使用红黑树等容器遍历文件统计IP的数量

当然, 经过哈希切割的海量数据, 可能也会出现问题：

海量数据绝大部分或者全部都只是同一个数据, 经过哈希切割出来的文件也是非常大的文件, 依旧存在海量数据的情况

此种情况在统计的时候不会发生太大的问题, 因为在使用红黑树等容器遍历文件统计数量时, 容器中只会存储一个数据, 当遍历过程中再次遇到此数据时, 容器中并不会再次存储, 而只是进行统计将计数进行++

所以, 不用担心此时会发生内存报错

发生哈希冲突, 即同一个文件中可能存在太多个不同的IP(太多表示依旧是海量数据)

当哈希切割之后, 同一个文件中依旧存在海量的不同IP, 又该怎么解决？

作者：哈米d1ch 发表日期：2023 年 2 月 20 日